1. 서론 (Introduction)
본 보고서는 현대 포트폴리오 이론(Modern Portfolio Theory, MPT)의 핵심인 평균-분산 결정법(Mean-Variance Analysis)을 부동산 투자 영역에 적용할 때의 의의와 한계점을 분석하는 것을 목적으로 합니다. 해리 마코위츠(Harry Markowitz)에 의해 개발된 평균-분산 결정법은 투자의 기대수익률(평균)과 위험(분산)을 동시에 고려하여 최적의 투자 포트폴리오를 구성하는 이론적 틀을 제공합니다. 부동산 투자 역시 여러 자산에 분산하여 포트폴리오를 구성할 수 있으므로, 이 방법론의 적용 가능성과 함께 부동산 자산의 고유한 특성으로 인해 발생하는 적용상의 한계점 또는 오류(Mean-Variance Error/Limitations)를 중점적으로 검토하고자 합니다.

2. 평균-분산 결정법의 개요 (Overview of Mean-Variance Analysis)
평균-분산 결정법은 다음과 같은 핵심 개념에 기반하여 투자자가 최적의 위험-수익 상쇄관계(Risk-Return Trade-off)를 달성하는 포트폴리오를 선택하도록 돕습니다.
- 기대수익률 (평균, Mean): 해당 자산 또는 포트폴리오로부터 미래에 얻을 것으로 예상되는 평균적인 수익률입니다.
- 위험 (분산/표준편차, Variance/Standard Deviation): 수익률의 변동성 또는 불확실성을 측정하는 지표입니다. 분산(또는 표준편차)이 클수록 위험이 높다고 간주합니다.
- 상관계수 (Correlation): 포트폴리오를 구성하는 각 자산들의 수익률이 서로 어떻게 움직이는지를 나타내는 지표입니다. 상관계수가 낮거나 음(-)일수록 분산투자 효과가 커집니다.
- 분산투자 (Diversification): 상관관계가 낮은 여러 자산에 나누어 투자함으로써, 포트폴리오 전체의 위험을 개별 자산 위험의 단순 합보다 낮추는 전략입니다.
- 효율적 투자선 (Efficient Frontier): 주어진 위험 수준에서 최고의 기대수익률을 제공하거나, 주어진 기대수익률 수준에서 최소의 위험을 부담하는 포트폴리오들의 집합을 그래프 상에 나타낸 선입니다.
- 최적 포트폴리오 (Optimal Portfolio): 효율적 투자선 상에 있는 포트폴리오 중에서 특정 투자자의 위험 선호도(위험 감수 성향)와 일치하는 포트폴리오입니다.
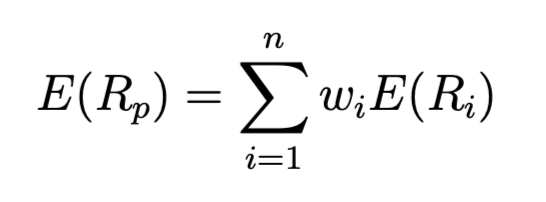
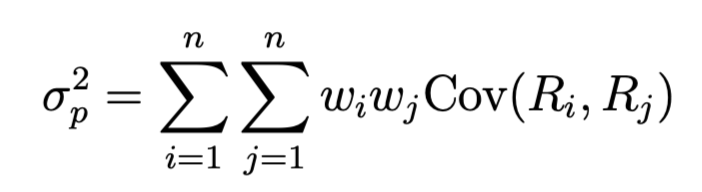
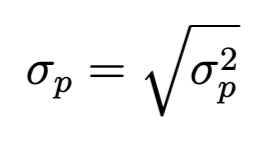
3. 부동산 투자 포트폴리오에의 적용 (Application to Real Estate Investment Portfolios)
평균-분산 결정법의 원리는 개별 부동산 자산이나 부동산 관련 증권(예: 리츠(REITs), 부동산 펀드)으로 구성된 포트폴리오에 개념적으로 적용될 수 있습니다.
적용 방식: 다양한 지역(수도권/지방 등), 다양한 용도(주거용/상업용/산업용 등), 다양한 개발 단계(안정된 임대 자산/개발 프로젝트 등)의 부동산 자산 또는 관련 금융 상품에 분산 투자하는 포트폴리오를 구성할 때, 각 자산(또는 자산군)의 기대수익률, 위험(변동성), 그리고 상호 간의 상관관계를 추정하여 효율적 투자선을 도출하고 최적의 자산 배분 비율을 결정하는 데 활용될 수 있습니다.
기대 효익: 위험과 수익을 정량적으로 고려하여 체계적인 포트폴리오 구축을 가능하게 하고, 분산투자의 중요성을 강조하며, 감정에 치우치지 않는 합리적인 투자 결정을 지원할 수 있습니다.
4. 평균-분산 결정법의 한계 및 오류 (Limitations and "Errors" of Mean-Variance Analysis in Real Estate)
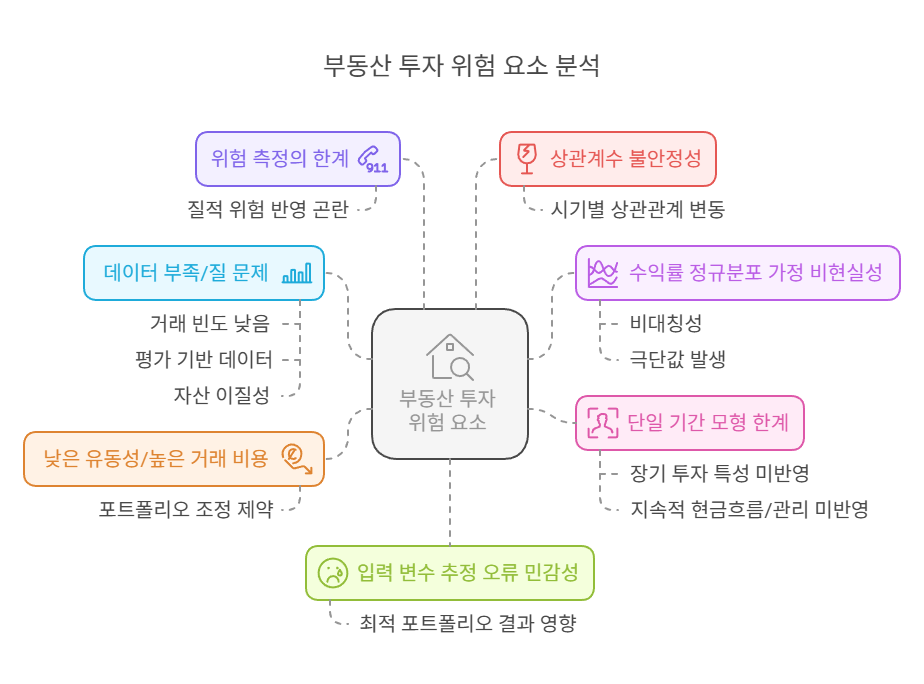
이론적으로 유용함에도 불구하고, 평균-분산 결정법을 부동산 투자에 직접 적용하는 데에는 다음과 같은 심각한 한계점, 즉 모델 가정과 부동산 현실 간의 불일치에서 오는 오류(Shortcomings)가 존재합니다.
- 데이터의 부족 및 질적 문제 (Data Scarcity and Quality Issues):
- 낮은 거래 빈도 및 가격 정보 부족: 개별 부동산은 주식처럼 빈번하게 거래되지 않으므로, 신뢰할 수 있는 과거 시계열 수익률 데이터를 확보하기 어렵습니다. 이는 정확한 기대수익률, 분산, 상관관계 추정을 매우 어렵게 만듭니다.
- 평가 기반 데이터의 한계 (Appraisal Smoothing): 부동산 가치 평가는 감정평가에 의존하는 경우가 많은데, 이는 실제 시장 변동성보다 완만하게(smoothed) 나타나는 경향이 있어 위험(분산)을 과소평가하게 만들 수 있습니다.
- 자산의 이질성 (Heterogeneity): 모든 부동산은 고유한 특성(위치, 건물 상태 등)을 가지므로, 특정 부동산의 과거 데이터가 다른 부동산의 미래를 예측하는 데 한계가 있습니다. 대표성 있는 데이터를 구축하기 어렵습니다.
- 수익률 정규분포 가정의 비현실성 (Unrealistic Assumption of Normal Distribution):
- 평균-분산 모형은 종종 자산 수익률이 정규분포(종 모양)를 따른다고 가정합니다. 그러나 부동산 시장 수익률은 비대칭성(Skewness)을 보이거나 극단적인 사건(꼬리 위험, Fat Tails)이 정규분포 가정보다 더 자주 발생하는 경향(첨도, Kurtosis)이 있습니다. 따라서 분산만으로는 실제 투자자가 직면하는 하락 위험(Downside Risk)을 충분히 포착하지 못할 수 있습니다.
- 낮은 유동성 및 높은 거래 비용 문제 (Low Liquidity and Transaction Costs):
- 평균-분산 모형은 포트폴리오를 최적 상태로 유지하기 위해 필요시 자산을 쉽게 매매하여 리밸런싱(Rebalancing)할 수 있다고 암묵적으로 가정합니다. 하지만 부동산은 유동성이 매우 낮고 거래 비용(세금, 중개수수료 등)이 높아 원하는 시점에 적정 가격으로 신속하게 거래하거나 포트폴리오를 조정하기가 매우 어렵습니다.
- 위험 측정의 한계 (Limitations of Risk Measurement):
- 위험을 수익률의 분산(변동성)으로만 측정하는 것은 하락 위험에 대한 투자자의 실제 우려를 제대로 반영하지 못할 수 있습니다. 또한, 임차인 부도 위험, 공실 위험, 법적 분쟁 위험, 특정 건물의 물리적 결함 등 정량화하기 어려운 질적 위험 요소들을 모형에 통합하기 어렵습니다.
- 상관계수의 불안정성 (Instability of Correlations):
- 분산투자의 효과는 자산 간 상관계수에 크게 의존하는데, 부동산 자산 간 또는 부동산과 다른 자산 간의 상관계수는 시간에 따라, 특히 시장 상황(예: 금융 위기)에 따라 크게 변동할 수 있습니다. 이는 포트폴리오의 실제 위험 분산 효과가 기대와 다를 수 있음을 의미합니다.
- 입력 변수 추정 오류 민감성 (Sensitivity to Input Estimation Errors):
- 평균-분산 모형의 결과(최적 포트폴리오 구성)는 입력 변수(기대수익률, 분산, 상관계수)의 작은 추정 오류에도 매우 민감하게 변동하는 경향이 있습니다. 부정확한 데이터로 인한 추정 오류는 잘못된 투자 결정으로 이어질 수 있습니다.
- 단일 기간 모형의 한계 (Limitations of Single-Period Model):
- 전통적인 평균-분산 모형은 주로 단일 투자 기간을 가정하지만, 부동산 투자는 일반적으로 장기간에 걸쳐 이루어지며 지속적인 현금 흐름(임대료)과 관리 결정을 수반합니다. 이러한 다기간(Multi-period) 특성을 단순 모형이 제대로 반영하기 어렵습니다.
5. 결론 및 시사점 (Conclusion and Implications)
평균-분산 결정법은 부동산 투자 포트폴리오를 구성하는 데 있어 분산투자의 중요성과 위험-수익 관계를 고려하는 중요한 이론적 틀을 제공합니다. 투자 결정을 보다 체계적이고 정량적으로 접근하도록 돕는다는 점에서 의의가 있습니다.
하지만 위에서 살펴본 바와 같이, 부동산 자산의 고유한 특성(데이터 부족, 이질성, 낮은 유동성, 비정규분포 수익률 등)은 평균-분산 모형의 핵심 가정을 위배하는 경우가 많아 이론을 현실에 직접 적용하는 데에는 상당한 주의와 제약이 따릅니다. 이러한 적용상의 한계 또는 '오류' 가능성을 인지하지 못하고 모형 결과만을 맹신하는 것은 위험합니다.
따라서 실제 부동산 투자 의사결정 시에는 평균-분산 분석 결과를 하나의 참고 자료로 활용하되, 데이터의 한계를 인식하고 정성적인 분석, 시나리오 분석, 대체 위험 측정 방법 등을 병행하는 것이 바람직합니다. 즉, 정량적 모델의 통찰력과 함께 투자자의 경험, 시장 상황에 대한 깊이 있는 이해, 그리고 현실적인 제약 조건들을 종합적으로 고려하는 균형 잡힌 접근이 요구됩니다.
[부동산] 부동산 주요개념 총정리
부동산에 대한 개념을 이해하기 쉽게 올리고 있습니다. 여러분 모두 올해는 성공적인 한 해가 되시길 기원하는 마음으로 작성하였습니다. 페이지를 즐겨찾기하여 더 많은 정보를 얻어가실 수
jkcb.tistory.com
이어지는 아래의 글에서는 위에서 다룬 내용을 좀더 깊게 다루고 있습니다.
I. 서론
1.1. 연구의 목적 및 중요성
부동산 투자는 잠재적으로 높은 수익을 기대할 수 있는 매력적인 투자 수단이지만, 동시에 다양한 위험 요소를 내포하고 있어 복잡한 의사결정 과정을 요구한다. 성공적인 부동산 투자를 위해서는 단순히 기대되는 수익률뿐만 아니라, 투자 대상에 내재된 다양한 위험을 정확하게 평가하고, 그 위험을 감수하는 대가로 합리적인 수준의 보상을 요구하는 체계적인 분석이 필수적이다. 투자자는 예상되는 미래 수익과 현재의 확실한 소비 사이에서 신중한 선택을 내려야 하며, 이 과정에서 위험과 수익 간의 관계를 명확히 이해하는 것이 무엇보다 중요하다.
본 보고서는 부동산 투자 의사결정의 근간을 이루는 핵심 원리인 위험-수익 상쇄관계(Risk-Return Tradeoff)를 심층적으로 분석하는 데 목적을 둔다. 투자자가 감수하는 위험의 수준이 기대하는 수익률에 어떻게 영향을 미치는지, 그리고 이 과정에서 무위험수익률, 위험할증률, 인플레이션과 같은 주요 금융 개념들이 부동산 투자 맥락에서 어떻게 작용하는지를 체계적으로 설명하고자 한다. 이를 통해 투자자들이 보다 합리적이고 정보에 기반한 의사결정을 내리는 데 기여하고자 한다.
1. 평균-분산 결정법(MVD)의 기초
1.1. 핵심 개념: 투자 이론에서의 위험-수익 최적화
평균-분산 결정법(Mean-Variance Decision Rule, MVD)은 해리 마코위츠(Harry Markowitz)에 의해 개발된 현대 포트폴리오 이론(Modern Portfolio Theory, MPT)의 초석을 이루는 분석 틀이다. 이 방법론의 근본적인 목표는 주어진 위험 수준 하에서 기대수익률을 극대화하거나, 주어진 기대수익률 수준에서 위험을 최소화하는 투자 포트폴리오를 구성하는 데 있다.
MVD는 투자의사결정을 내리는 데 있어 두 가지 핵심적인 통계적 측정치, 즉 기대수익률(평균)과 위험(분산 또는 표준편차)에 기반한다. 여기서 '평균'은 투자로부터 예상되는 수익률의 중심 경향을 의미하며, '분산' 또는 그 제곱근인 '표준편차'는 예상 수익률로부터 실제 수익률이 벗어날 가능성, 즉 변동성을 측정하는 지표로 사용된다. 중요한 점은 MVD가 투자의 가치를 평가하고 대안을 선택하는 데 있어 오직 이 두 가지 통계적 모수만을 고려한다는 것이다. 이러한 단순화는 MVD를 강력한 이론적 도구로 만들었지만, 동시에 현실 적용에서의 한계점을 내포하게 되는 원인이 되기도 한다.
MVD가 최적화하고자 하는 핵심은 본질적으로 위험과 수익 간의 상충관계(risk-return trade-off)이다. 일반적으로 투자 세계에서는 더 높은 잠재적 수익을 얻기 위해서는 더 높은 수준의 위험을 감수해야 한다. MVD는 이러한 상충관계를 정량적으로 분석하여 투자자가 자신의 위험 선호도에 맞는 최적의 균형점을 찾도록 돕는다.
MVD 프레임워크는 개별 자산의 위험과 수익률 자체보다는 해당 자산이 전체 포트폴리오의 위험과 수익률에 어떻게 기여하는지에 초점을 맞춤으로써 투자 분석의 패러다임을 전환시켰다. 마코위츠의 핵심 통찰은 개별 자산의 위험(분산) 그 자체보다 다른 자산과의 공분산(covariance) 또는 상관관계(correlation)가 포트폴리오 전체 위험에 더 중요하다는 점이었다. MPT 이전에는 투자자들이 개별 자산의 특성에 집중하는 경향이 있었으나, MPT와 MVD는 포트폴리오 내 자산 간의 상호작용을 고려하는 시스템적 관점을 제시했다. 즉, 자산 간의 상관관계가 완벽하게 양(+)이 아닐 경우(상관계수 < 1), 자산들을 결합함으로써 개별 자산 위험의 단순 가중평균보다 낮은 포트폴리오 위험을 달성할 수 있다는 분산투자(diversification)의 효과를 수학적으로 증명한 것이다. 이는 개별적으로는 위험해 보이는 자산이라 할지라도 다른 자산과 음(-)의 상관관계를 가진다면 오히려 전체 포트폴리오의 위험을 줄이는 데 기여할 수 있음을 의미한다. 이러한 관점의 변화는 MVD의 강력함과 동시에 정확한 공분산 추정의 중요성을 부각시킨다.
1.2. 지배원리(Dominance Principle) 설명
지배원리는 MVD 프레임워크 내에서 투자 대안을 선택하는 핵심적인 메커니즘이다. 이 원리는 두 가지 간단한 규칙으로 구성된다:
- 동일한 위험 수준(분산 또는 표준편차)에서는 기대수익률이 가장 높은 투자안을 선택한다.
- 동일한 기대수익률 수준에서는 위험(분산 또는 표준편차)이 가장 낮은 투자안을 선택한다.
예를 들어, 투자안 A와 B의 기대수익률이 모두 10%이지만, A의 표준편차가 5%이고 B의 표준편차가 7%라면, 지배원리에 따라 투자자는 위험이 더 낮은 A를 선택할 것이다(A가 B를 지배한다). 반대로, 투자안 C와 D의 표준편차가 모두 8%이지만, C의 기대수익률이 12%이고 D의 기대수익률이 10%라면, 투자자는 기대수익률이 더 높은 C를 선택할 것이다(C가 D를 지배한다).
이 지배원리는 여러 투자 대안 중에서 비효율적인(inefficient) 투자안, 즉 동일한 위험 수준에서 더 낮은 수익을 제공하거나 동일한 수익 수준에서 더 높은 위험을 감수해야 하는 투자안을 걸러내는 역할을 한다. 결과적으로 지배원리를 통해 선택된 투자안들은 주어진 위험 수준에서 최상의 기대수익률을 제공하거나, 주어진 기대수익률 수준에서 최소의 위험을 부담하는, 소위 '효율적인(efficient)' 투자안들의 집합을 형성하게 된다.
지배원리는 단순히 기계적인 분류 규칙이 아니라, MPT의 근간을 이루는 투자자의 행동 가정, 즉 위험 회피(risk aversion) 성향을 내포하고 있다. 지배원리의 두 규칙은 투자자들이 위험(변동성)을 싫어하고 수익(기대값)을 선호한다는 가정 하에서만 합리적이다. 즉, 합리적인 투자자는 더 많은 위험을 감수하는 대가로 더 높은 기대수익률이라는 보상을 요구하며, 불필요한 위험은 감수하려 하지 않는다는 것이다. 만약 투자자가 위험 자체를 추구하거나(risk-seeking) 위험에 무관심하다면(risk-neutral), 지배원리를 따를 이유가 없다. 따라서 지배원리는 MVD의 수학적 구조뿐만 아니라 그 이면에 깔린 합리적이고 위험 회피적인 투자자 행동 모델을 반영한다. 이는 MVD를 현실에 적용할 때, 실제 투자자들의 다양한 효용 함수나 행동 편향을 고려해야 하는 이유가 된다.
2. MVD를 활용한 포트폴리오 구성: 효율적 프론티어
2.1. MVD 내에서의 분산투자 논리
MVD는 분산투자의 이점을 수학적으로 명확하게 보여준다. 포트폴리오의 전체 위험(분산)은 개별 자산들의 위험(분산)뿐만 아니라, 결정적으로 자산들 간의 공분산(covariance) 또는 상관계수(correlation coefficient)에 의해 영향을 받는다.
핵심 원리는 상관관계가 낮거나 음(-)인 자산들을 결합할 경우, 개별 자산 위험의 단순 가중평균보다 낮은 수준의 포트폴리오 위험을 달성할 수 있다는 것이다. 이는 각 자산의 수익률 변동이 서로 상쇄되는 효과 때문이다. 예를 들어, 두 자산(A, B)으로 구성된 포트폴리오의 분산(σ²p)은 다음과 같이 표현될 수 있다:
σ²p = wA²σA² + wB²σB² + 2wAwB Cov(A, B)
(또는 Cov(A, B) = ρAB σA σB 를 이용하여)
σ²p = wA²σA² + wB²σB² + 2wAwB ρAB σA σB
여기서 w는 투자 비중, σ²는 분산, Cov는 공분산, ρ는 상관계수를 나타낸다. 상관계수(ρAB)가 +1보다 작을수록 (특히 음수일수록) 세 번째 항의 기여도가 작아지거나 음수가 되어 전체 포트폴리오 분산(σ²p)이 감소하게 된다. 상관계수가 -1이면 이론적으로 위험을 완전히 제거하는 것도 가능하다 (물론 현실에서는 거의 불가능하다).
MVD는 투자 위험을 크게 두 가지로 구분한다. 첫째는 체계적 위험(systematic risk) 또는 시장 위험(market risk)으로, 이는 경제 전반의 상황 변화(예: 경기 변동, 인플레이션, 이자율 변동 등)에 따라 시장의 모든 자산에 영향을 미치는 위험이다. 이 위험은 분산투자를 통해서도 제거할 수 없다. 둘째는 비체계적 위험(unsystematic risk) 또는 특정 위험(specific risk)으로, 이는 개별 기업이나 자산의 고유한 요인(예: 경영 능력, 신제품 실패, 특정 부동산의 입지 변화 등)으로 인해 발생하는 위험이다. 이 위험은 서로 다른 자산들을 조합하는 분산투자를 통해 상당 부분 감소시키거나 제거할 수 있다. MPT와 MVD의 주요 목표 중 하나는 바로 이 비체계적 위험을 효율적으로 제거하는 것이다.
MVD 하에서 분산투자의 효과는 자산 간 상관관계 추정치의 정확성에 크게 의존한다. 분산투자의 핵심 이점은 수익률 움직임이 서로 다른 자산들을 결합하는 데서 나오기 때문에, 만약 상관관계 추정이 부정확하다면(예: 과거 데이터가 미래 관계를 반영하지 못하거나, 비선형적 의존성을 포착하지 못하는 경우), 예측된 분산 효과는 실제와 다를 수 있다. 이는 특히 거래 빈도가 낮고 감정평가 평활화(appraisal smoothing) 문제에 노출된 부동산과 같은 자산의 경우, 상관관계를 정확하게 측정하기 어렵기 때문에 실무적으로 중요한 제약이 된다.
2.2. 효율적 프론티어(Efficient Frontier) 구축
효율적 프론티어는 MVD 분석의 결과를 시각적으로 나타내는 핵심 개념이다. 이는 주어진 각 위험 수준(표준편차)에 대해 달성 가능한 가장 높은 기대수익률을 제공하는 포트폴리오들의 집합, 또는 주어진 각 기대수익률 수준에 대해 가장 낮은 위험을 갖는 포트폴리오들의 집합을 의미한다. 즉, 지배원리에 의해 선택된 효율적인 포트폴리오들을 연결한 선이다.
기대수익률(Y축)과 위험(표준편차, X축)으로 구성된 2차원 평면에서 효율적 프론티어는 일반적으로 우상향하면서 위로 볼록한(concave) 곡선 형태를 띤다. 이는 위험이 증가함에 따라 추가적인 위험 단위당 얻을 수 있는 기대수익률의 증가분(한계수익률)이 점차 감소하는 경향(수확 체감)을 반영한다. 효율적 프론티어 상에서 가장 왼쪽에 위치하여 변동성이 가장 낮은 포트폴리오를 최소분산 포트폴리오(Minimum Variance Portfolio, MVP)라고 한다.
효율적 프론티어 상의 특정 포트폴리오들은 수학적 최적화 기법을 통해 계산된다. 이 과정에서는 각 자산의 기대수익률, 분산, 그리고 자산 간 공분산(또는 상관관계) 추정치를 입력값으로 사용하여, 특정 제약 조건(예: 목표 기대수익률, 총 투자 비중 합계 1) 하에서 포트폴리오의 분산을 최소화하는 각 자산의 최적 투자 비중(weights)을 찾아낸다.
효율적 프론티어의 구체적인 위치와 형태는 분석 대상이 되는 자산 집합과 사용된 입력값 추정치(기대수익률, 분산, 공분산)에 전적으로 의존한다. 즉, 효율적 프론티어는 보편적인 개념이 아니라 분석되는 투자 유니버스에 따라 달라진다. 예를 들어, 기존 포트폴리오에 새로운 자산군(예: 부동산)을 추가할 경우, 만약 해당 자산이 기존 자산들과 낮은 상관관계를 보여 분산투자 효과를 제공한다면, 효율적 프론티어는 기존보다 더 우상향으로 이동하여 더 나은 위험-수익 기회를 제공할 수 있다. 그러나 앞서 언급했듯이, 입력값 추정치의 오류는 효율적 프론티어 자체를 잘못된 위치에 그리게 만들 수 있으며, 특히 MVD의 결과는 입력값 변화에 매우 민감하게 반응하는 경향이 있어 최적화 결과의 신뢰성을 떨어뜨릴 수 있다.
2.3. 최적 포트폴리오 선택: 투자자 위험 선호도의 역할
효율적 프론티어는 여러 효율적인 포트폴리오의 집합을 제시할 뿐, 특정 투자자에게 가장 적합한 단 하나의 '최적' 포트폴리오를 결정해주지는 않는다. 최적 포트폴리오의 선택은 궁극적으로 개별 투자자의 위험 선호도(risk preference) 또는 위험 회피도(risk aversion)에 따라 달라진다.
투자자의 위험 선호도는 무차별곡선(indifference curve)이라는 개념을 통해 표현될 수 있다. 무차별곡선은 투자자에게 동일한 수준의 효용(만족도)을 제공하는 위험(표준편차)과 기대수익률의 조합들을 연결한 선이다. 일반적으로 위험 회피적인 투자자의 무차별곡선은 우상향하며 원점에 대해 볼록한(convex to the origin) 형태를 가진다. 우상향하는 이유는 더 높은 위험을 감수할 때 동일한 효용을 유지하기 위해 더 높은 기대수익률을 요구하기 때문이며, 원점에 대해 볼록한 이유는 위험이 증가할수록 추가적인 위험 단위당 요구하는 보상(기대수익률 증가분)이 더 커지기 때문이다.
투자자는 자신이 도달할 수 있는 가장 높은 수준의 효용을 주는 무차별곡선을 선호한다. 따라서 특정 투자자의 최적 포트폴리오는 그 투자자의 무차별곡선 중 가장 높은 효용 수준을 나타내는 곡선이 효율적 프론티어와 접하는(tangent) 지점에서 결정된다. 이 접점은 투자자가 주어진 효율적인 투자 기회 집합(효율적 프론티어) 내에서 자신의 효용을 극대화하는 포트폴리오를 의미한다.
투자자의 위험 회피도에 따라 무차별곡선의 기울기는 달라진다. 위험 회피도가 높은 (보수적인) 투자자는 무차별곡선의 기울기가 가파르며, 효율적 프론티어 상에서 상대적으로 낮은 위험과 낮은 기대수익률을 갖는 포트폴리오를 선택하게 된다. 반면, 위험 회피도가 낮은 (공격적인) 투자자는 무차별곡선의 기울기가 완만하며, 효율적 프론티어 상에서 더 높은 위험과 더 높은 기대수익률을 갖는 포트폴리오를 선택하게 된다.
MVD 프레임워크에서 무위험 자산(risk-free asset)의 존재 여부는 최적 포트폴리오 선택 과정에 근본적인 변화를 가져온다. 무위험 자산이란 수익률의 변동성이 0이고 다른 모든 자산과의 상관관계도 0인 이론적인 자산으로, 현실에서는 정부 발행 단기 국채(예: 미국 T-bill) 등이 근사치로 사용된다. 무위험 자산이 존재하고 투자자가 이 자산을 자유롭게 차입하거나 대출할 수 있다고 가정하면, 효율적 투자 기회 집합은 더 이상 곡선 형태의 효율적 프론티어가 아니라, 무위험 자산 수익률(Y절편)에서 시작하여 기존의 위험자산 효율적 프론티어에 접하는 직선, 즉 자본배분선(Capital Allocation Line, CAL)이 된다. 이 경우, 모든 위험 회피적인 투자자는 위험 선호도와 관계없이 동일한 구성의 위험자산 포트폴리오, 즉 CAL과 기존 효율적 프론티어의 접점 포트폴리오(tangency portfolio)를 보유하게 된다. 투자자들은 자신의 위험 선호도에 따라 이 접점 포트폴리오와 무위험 자산 간의 투자 비중만을 조절하여 전체 포트폴리오의 위험과 수익을 결정한다. 이를 토빈의 분리정리(Tobin's Separation Theorem) 또는 이펀드 분리(Two-Fund Separation)라고 한다. 이는 투자 결정 과정을 '최적 위험 포트폴리오 선택'과 '위험 수준 결정'의 두 단계로 분리하여 단순화시키는 중요한 이론적 의미를 갖는다. 그러나 이 역시 무위험이자율로 무제한적인 차입과 대출이 가능하다는 비현실적인 가정에 기반한다는 한계가 있다.
3. 평균-분산 프레임워크의 기본 가정
평균-분산 결정법(MVD)은 특정 가정들에 기반하여 구축된 이론적 모델이다. 이러한 가정들을 이해하는 것은 MVD의 강점과 약점, 그리고 현실 적용의 한계를 파악하는 데 필수적이다.
3.1. 투자자 행동: 합리성과 위험 회피
- 합리성(Rationality) 가정: MVD는 투자자들이 합리적으로 행동한다고 가정한다. 즉, 투자자들은 이용 가능한 모든 정보를 바탕으로 자신의 기대 효용(expected utility)을 극대화하기 위해 논리적인 의사결정을 내린다. 이들은 일관되게 지배원리를 따라 투자 대안을 선택한다.
- 위험 회피(Risk Aversion) 가정: MVD는 투자자들이 위험 회피적이라고 가정한다. 이는 투자자들이 위험(수익률의 변동성 또는 분산)을 싫어하며, 추가적인 위험을 감수하기 위해서는 그에 상응하는 더 높은 기대수익률을 요구한다는 의미이다. 즉, 투자자의 효용은 기대수익률에 대해서는 증가하지만, 위험에 대해서는 감소한다.
함의: 이러한 투자자 행동 가정은 MVD가 왜 기대수익률(평균)과 위험(분산)이라는 두 가지 지표에만 초점을 맞추는지를 정당화하며, 앞서 설명한 무차별곡선의 형태(우상향하며 원점에 대해 볼록)를 뒷받침한다.
비판: 현실 세계의 투자자들은 종종 순수한 합리성에서 벗어난 행동을 보인다. 행동 재무학(behavioral finance) 연구들은 투자자들이 손실 회피(loss aversion), 앵커링(anchoring), 군집 행동(herding), 과신(overconfidence) 등 다양한 인지적, 감정적 편향에 영향을 받는다는 것을 보여준다. 예를 들어, 손실 회피 성향은 투자자들이 잠재적 손실에 대해 잠재적 이익보다 훨씬 더 민감하게 반응하게 만들어, MVD가 예측하는 것과 다른 투자 결정을 내리게 할 수 있다. 이러한 행동적 요인들은 MVD의 기본 가정을 약화시킨다.
3.2. 시장 조건: 마찰 없는 시장, 정보 가용성
- 마찰 없는 시장(Frictionless Markets) 가정: MVD는 시장에 거래 비용(예: 중개 수수료, 매수-매도 호가 스프레드)이나 세금과 같은 마찰 요인이 존재하지 않는다고 가정한다.
- 자산의 완전 분할 가능성(Perfect Divisibility) 가정: 투자자는 어떤 자산이든 원하는 만큼의 작은 단위로 사고팔 수 있다고 가정한다.
- 정보의 완전성 및 효율적 시장(Perfect Information & Efficient Markets) 가정: 모든 관련 정보는 모든 투자자에게 즉시, 그리고 무료로 제공되며, 시장 가격은 이 모든 정보를 완전히 반영한다고 가정한다 (효율적 시장 가설).
- 무제한 차입/대출 가정 (무위험 자산 존재 시): 투자자들은 단일한 무위험이자율로 원하는 만큼 자유롭게 자금을 빌리거나 빌려줄 수 있다고 가정한다.
비판: 특히 부동산 시장은 이러한 가정들과 큰 괴리를 보인다. 부동산 거래에는 상당한 거래 비용(중개 수수료, 취득세, 법무 비용 등)이 수반된다. 부동산 자산은 주식과 달리 쉽게 분할하기 어렵다 (불가분성). 부동산 시장은 정보 비대칭성이 높고 투명성이 낮아 시장 비효율성이 존재할 가능성이 크다. 또한, 모든 투자자가 동일한 무위험이자율로 무제한 차입 및 대출을 할 수 있다는 가정 역시 현실과 동떨어져 있다. 이러한 현실적 제약들은 MVD 모델의 직접적인 적용을 어렵게 만든다.
3.3. 수익률 분포: 정규분포 가정
- 정규분포(Normality) 가정: MVD의 가장 핵심적인 통계적 가정 중 하나는 자산의 수익률이 정규분포(Normal Distribution 또는 Gaussian Distribution)를 따른다는 것이다. 정규분포는 평균을 중심으로 좌우 대칭인 종 모양의 분포를 의미한다.
함의: 이 가정이 성립하면, 수익률 분포의 모든 통계적 특성은 오직 평균(기대수익률)과 분산(위험)이라는 두 개의 모수(parameter)만으로 완벽하게 설명될 수 있다. 따라서 위험을 분산 또는 표준편차만으로 측정하는 것이 정당화되며, 포트폴리오 최적화 계산이 상대적으로 단순해진다.
비판: 그러나 수많은 실증 연구들은 금융 자산 수익률, 특히 부동산과 같은 비유동성 자산의 수익률 분포가 정규분포 가정을 따르지 않는 경우가 많다는 것을 보여준다. 주요 편차는 다음과 같다:
- 왜도(Skewness): 수익률 분포가 평균을 중심으로 대칭적이지 않은 경우를 의미한다. 예를 들어, 음(-)의 왜도를 가지는 경우, 평균보다 낮은 수익률(큰 손실)이 평균보다 높은 수익률보다 더 자주 또는 더 극단적으로 발생할 수 있다. 부동산 시장의 하락 국면에서 큰 폭의 가격 하락 가능성을 고려할 때, 부동산 수익률은 음의 왜도를 보일 수 있다.
- 첨도(Kurtosis) 및 팻 테일(Fat Tails): 실제 수익률 분포는 정규분포보다 중심 부분이 더 뾰족하고 꼬리 부분이 더 두꺼운 형태(leptokurtosis)를 보이는 경우가 많다. 이는 평균에서 멀리 떨어진 극단적인 수익률(매우 큰 이익 또는 매우 큰 손실)이 정규분포가 예측하는 것보다 훨씬 더 높은 확률로 발생할 수 있음을 의미한다. '블랙 스완' 이벤트와 같은 예상치 못한 시장 충격의 가능성은 팻 테일 현상으로 설명될 수 있다.
수익률의 정규분포 가정은 MVD를 부동산과 같이 비정규적 수익률 특성을 보이는 자산에 적용할 때 심각한 문제점을 야기한다. 만약 수익률이 정규분포를 따르지 않는다면, 분산은 위험을 완전히 포착하지 못하는 불완전한 측정치가 된다. 특히, 투자자들이 가장 우려하는 극단적인 손실 가능성(팻 테일)이나 분포의 비대칭성(왜도)을 제대로 반영하지 못한다. 투자자들은 단순히 전체적인 변동성(분산)보다는 특정 목표 수익률 이하로 하락할 위험(downside risk)에 더 민감할 수 있는데, 분산은 이러한 하방 위험과 상방 변동성을 동일하게 취급한다. 따라서 비정규 분포 환경에서 분산에만 의존하는 MVD는 투자자가 직면하는 실제 위험, 특히 부동산 시장과 같이 비유동적이고 간헐적으로 큰 폭의 가격 변동이 나타날 수 있는 시장에서의 위험을 과소평가할 수 있다. 이는 MVD를 통해 도출된 효율적 프론티어와 최적 포트폴리오의 신뢰성에 근본적인 의문을 제기한다.
4. 비판적 분석: 평균-분산 오류 및 부동산 투자 적용의 한계점
평균-분산 결정법(MVD)은 포트폴리오 이론의 발전에 크게 기여했지만, 특히 부동산과 같이 독특한 특성을 지닌 자산군에 적용할 때는 여러 가지 한계점과 오류 가능성("평균-분산 오류")을 드러낸다.
4.1. 부동산 수익률 분포의 문제점
4.1.1. 비정규성: 부동산 수익률의 왜도 및 팻 테일
앞서 언급했듯이, 부동산 수익률은 종종 정규분포에서 벗어나는 특성을 보인다. 이는 MVD 적용의 근본적인 한계를 야기한다. 시장의 비유동성으로 인해 거래가 뜸하다가 갑자기 큰 폭의 가격 변동이 발생하거나, 레버리지 사용으로 인해 이익과 손실이 비대칭적으로 증폭되는 현상, 그리고 부동산 시장의 뚜렷한 경기 순환 주기 등은 수익률 분포의 비정규성을 유발하는 요인이 될 수 있다. 일부 연구들은 부동산 수익률 분포가 정규분포 가정을 충족하지 못하며, 특히 왜도(skewness)나 첨도(kurtosis) 측면에서 차이를 보인다는 점을 지적한다.
이러한 비정규성은 MVD 적용에 심각한 문제를 일으킨다. MVD는 위험을 오직 분산(또는 표준편차)으로만 측정하는데, 비정규 분포 하에서는 분산이 전체 위험을 충분히 설명하지 못하기 때문이다. 특히, 투자자들이 우려하는 급격한 가격 하락과 같은 극단적인 사건의 발생 가능성(팻 테일)이나 손실 가능성의 비대칭성(왜도)을 분산은 제대로 포착하지 못한다. 결과적으로 MVD는 부동산 투자의 실제 위험, 특히 하방 위험(downside risk)이나 꼬리 위험(tail risk)을 과소평가할 수 있다.
4.1.2. 감정평가 평활화(Appraisal Smoothing)가 변동성 및 상관관계에 미치는 영향
부동산, 특히 비상장 상업용 부동산이나 사모 부동산 펀드의 수익률은 시장에서 빈번하게 거래되는 가격이 아니라 주기적인 감정평가(appraisal)에 기반하여 산출되는 경우가 많다. 이 과정에서 감정평가 평활화 현상이 발생하는데, 이는 감정평가액이 실제 시장 가치 변동보다 느리게 움직이며 변동성이 완만하게 나타나는 경향을 의미한다. 감정평가사들이 과거 평가액이나 비교 가능한 거래 사례에 의존하고, 보수적인 평가 경향을 보이는 등의 이유로 발생한다.
평활화 현상은 MVD 분석에 사용되는 입력 데이터에 중대한 왜곡을 가져온다. 첫째, 부동산 자산의 실제 변동성, 즉 위험(분산 또는 표준편차)을 인위적으로 낮게 추정하게 만든다. 둘째, 실제 시장 가격 변동과의 시차로 인해 다른 유동성 자산(예: 주식, 채권)과의 상관관계를 실제보다 낮게 보이게 하여, 포트폴리오 내에서의 분산투자 효과를 과대평가하게 만들 수 있다. 더욱이 이러한 평활화의 정도는 시장 상황이나 불확실성 수준에 따라 시간에 따라 변할 수 있어, 단순히 평균적인 보정 계수를 적용하여 평활화 효과를 제거하기도 어렵다.
감정평가 평활화는 MVD 프레임워크 내에서 부동산 자산이 실제보다 더 매력적인 위험-수익 특성을 가진 것처럼 보이게 만드는 '환영(phantom)' 효과를 창출한다. 평활화로 인해 측정된 위험(분산)은 낮아지고, 동시에 비유동성 자산으로서 기대수익률에 유동성 프리미엄이 반영될 수 있으므로, MVD 최적화 과정에서 부동산 자산은 위험 대비 수익률이 높은 것으로 잘못 인식될 수 있다. 이는 결과적으로 MVD 기반 포트폴리오에서 부동산 자산에 대한 과도한 배분을 유발할 수 있으며, 투자자는 모델이 제시하는 것보다 실제로는 더 높은 위험에 노출될 수 있다.
아래 표 1은 MVD의 수익률 관련 가정과 실제 부동산 수익률 특성 간의 주요 차이점을 요약한 것이다.
표 1: MVD 수익률 가정 vs. 실제 부동산 수익률 특성
| 특징 | MVD 가정 | 실제 부동산 특성 | MVD 적용 시 함의 |
|---|---|---|---|
| 분포 형태 | 정규분포 (대칭) | 종종 왜곡됨, 팻 테일 존재 | 분산은 불완전한 위험 측정치, 하방/꼬리 위험 과소평가 |
| 변동성 | 일정/예측 가능 | 시간에 따라 변동, 평활화 영향 | 위험 과소평가, 상관관계 왜곡 |
| 데이터 빈도 | 높음 (예: 일별 주식) | 낮음 (예: 분기별 감정평가) | 추정 어려움, 평활화 효과 심화 |
| 자기상관성 | 독립성 가정 | 평활화로 인한 자기상관성 존재 가능성 | 표준적 시계열 모델 부적합 가능성 |
| 극단값(Outliers) | 발생 확률 낮음 | 정규분포보다 높은 발생 확률 (팻 테일) | 분산/표준편차 추정치 왜곡, 위험 과소평가 |
이 표는 MVD의 이론적 기반과 부동산 데이터의 현실 사이의 근본적인 불일치를 명확히 보여준다. 이는 부동산 고유의 자산 특성을 고려하기 이전에 이미 수익률 데이터 자체의 성격으로 인해 MVD 적용이 왜 어려운지를 설명하며, 이어지는 구체적인 한계점 논의의 배경을 제공한다.
4.2. 부동산 위험 측정 지표로서 분산/표준편차의 부적절성
MVD는 위험을 전적으로 분산 또는 표준편차로 측정하지만, 이러한 지표는 부동산 투자의 다면적인 위험을 포착하는 데 여러 한계를 지닌다.
4.2.1. 하방 위험(Downside Risk) 특정 실패
분산과 표준편차는 기대수익률을 중심으로 수익률이 얼마나 흩어져 있는지를 측정하는 지표이다. 이는 기대수익률보다 높은 수익률(긍정적 변동)과 낮은 수익률(부정적 변동)을 동일하게 취급한다. 그러나 대부분의 위험 회피적인 투자자들은 수익률의 상방 변동성보다는 하방 변동성, 즉 잠재적 손실 가능성에 훨씬 더 민감하다. 특히 부동산 투자는 레버리지 효과, 비유동성, 시장 침체 가능성 등으로 인해 큰 폭의 손실이 발생할 수 있는 잠재력을 가지고 있다. 이러한 상황에서 전체 변동성만을 측정하는 분산/표준편차는 투자자가 실제로 중요하게 생각하는 하방 위험을 제대로 반영하지 못할 수 있다.
4.2.2. 이상치(Outliers) 및 데이터 문제에 대한 민감성
분산과 표준편차는 계산 방식상 극단적인 값, 즉 이상치(outlier)에 매우 민감하게 반응한다. 부동산 시장에서는 드물지만 큰 폭의 가격 변동이 발생할 수 있는데, 이러한 소수의 극단적인 데이터 포인트가 전체 기간의 분산 또는 표준편차 추정치를 크게 부풀릴 수 있다. 또한, 부동산 데이터는 종종 거래 빈도가 낮고 감정평가 시점 간의 간격이 길어 데이터 자체가 부족하거나 시의성이 떨어질 수 있으며, 앞서 언급한 평활화 문제까지 겹쳐 정확한 분산 추정을 더욱 어렵게 만든다.
4.2.3. 비재무적 위험 반영의 한계
MVD는 본질적으로 수익률 데이터의 통계적 변동성에 초점을 맞춘다. 따라서 부동산 투자에 내재된 다양한 비재무적 또는 정성적 위험 요인들을 직접적으로 반영하기 어렵다. 이러한 위험들은 부동산 투자의 성패에 결정적인 영향을 미칠 수 있음에도 불구하고, 평균-분산 분석에서는 간과되기 쉽다. 주요 비재무적 위험들은 다음과 같다:
- 유동성 위험(Liquidity Risk): 부동산은 필요할 때 즉시, 그리고 원하는 가격에 현금화하기 어려운 대표적인 비유동성 자산이다. 시장 상황이 악화되면 매수자를 찾기 어렵거나, 급매(fire sale)를 통해 상당한 가격 할인을 감수해야 할 수 있다. 이는 포트폴리오 리밸런싱을 어렵게 만들고 예상치 못한 자금 필요 상황에 대한 대응 능력을 저하시킨다.
- 법률 및 규제 위험(Legal/Regulatory Risk): 정부의 정책 변화, 세법 개정, 토지이용규제(예: 용도지역 변경), 환경 규제 강화 등은 부동산의 가치와 수익성에 직접적인 영향을 미칠 수 있다. 이러한 위험은 예측하기 어렵고 통제 불가능한 경우가 많다.
- 운영 및 관리 위험(Operational/Management Risk): 부동산은 보유 기간 동안 지속적인 관리가 필요하다. 공실 발생, 임차인 문제(임대료 체납, 분쟁), 예상치 못한 수리 및 유지보수 비용 증가, 관리 비효율 등 운영상의 문제들은 현금 흐름과 수익률에 부정적인 영향을 미친다.
- 금융 위험(Financial Risk): 레버리지(부채) 사용에 따른 위험(원리금 상환 부담, 채무 불이행 가능성), 이자율 변동 위험(특히 변동금리 대출 시), 재융자(리파이낸싱) 위험(만기 시 유리한 조건으로 재융자가 어려울 위험) 등 자금 조달과 관련된 위험이다.
부동산 투자의 성공은 단순히 가격 변동성(분산)을 관리하는 것을 넘어선다. 운영 효율성, 임차인 신용도, 법규 준수, 재융자 능력, 자산 매각 용이성 등 다양한 요인이 복합적으로 작용한다. MVD는 (종종 평활화된) 가격 데이터에서 파생된 수익률 분산에만 초점을 맞춤으로써, 이러한 중요한 운영, 금융, 법률, 유동성 차원의 위험들을 간과한다. 따라서 MVD를 통해 최적화된 포트폴리오는 이론적으로는 효율적으로 보일 수 있으나, 실제로는 이러한 정량화되지 않은 위험에 매우 취약할 수 있다.
4.3. 부동산 고유 특성 통합의 어려움
MVD는 본질적으로 유동성이 높고, 표준화되어 있으며, 거래 비용이 낮은 금융 시장의 자산을 염두에 두고 개발되었다. 따라서 부동산 자산이 가진 고유한 물리적, 시장적 특성들을 MVD 프레임워크에 통합하는 데에는 여러 어려움이 따른다.
4.3.1. 비유동성 및 시장성 문제
부동산의 낮은 유동성은 MVD의 마찰 없는 시장 및 용이한 거래 가정을 정면으로 위배한다. 부동산을 매각하는 데는 상당한 시간과 노력이 소요되며, 이는 MVD가 가정하는 즉각적인 포트폴리오 조정(rebalancing)을 어렵게 만든다. 또한, 비유동성은 그 자체로 위험 요인이 된다. 예상치 못한 자금 수요가 발생했을 때 원하는 가격에 신속하게 매각하지 못하거나, 시장 침체 시 '울며 겨자 먹기'식의 급매를 해야 할 가능성이 존재한다.
4.3.2. 높은 거래 비용
부동산 거래에는 중개 수수료, 법무 비용, 취득세, 등록세, 감정평가 비용 등 다양한 거래 비용이 발생하며, 이는 총 거래 금액의 상당 부분을 차지할 수 있다. 이는 MVD의 '거래 비용 제로' 가정과 명백히 배치된다. 높은 거래 비용은 순수익률을 감소시킬 뿐만 아니라, MVD 최적화 결과에 따라 포트폴리오를 자주 조정하는 전략을 비현실적이고 비용 비효율적으로 만든다.
4.3.3. 자산의 이질성 및 비표준화
주식이나 채권과 달리, 부동산 자산은 개별성이 매우 강하다. 동일한 지역 내의 유사한 유형의 부동산이라 할지라도 위치, 건물 상태, 임차인 구성, 관리 상태 등에 따라 가치와 위험 특성이 크게 달라진다. 이러한 이질성(heterogeneity)은 '대표적인' 부동산 자산의 기대수익률, 위험, 다른 자산과의 공분산을 정확하게 추정하는 것을 매우 어렵게 만든다. 부동산 지수를 구성할 때도 이러한 이질성으로 인해 대표성 문제가 발생할 수 있다.
4.3.4. 정보 비대칭성 및 시장 비효율성
부동산 시장은 상장 주식 시장에 비해 정보의 투명성이 낮고 비대칭성이 존재하는 경우가 많다. 특정 부동산의 상태, 잠재적 문제점, 실제 거래 가격 등에 대한 정보가 모든 시장 참여자에게 동등하게 공개되지 않을 수 있다. 이는 MVD의 완전 정보 가정을 위배하며, 정보 우위에 있는 참여자와 그렇지 못한 참여자 간의 불균형을 야기하고 시장 가격이 자산의 진정한 가치를 정확히 반영하지 못하는 비효율성을 초래할 수 있다.
4.3.5. 자산의 불가분성 및 포트폴리오 구성 제약
부동산 자산은 일반적으로 투자 단위가 크고, 주식처럼 소액으로 분할하여 투자하기 어렵다 (불가분성). 이러한 '덩어리진(lumpy)' 특성은 MVD 최적화 결과가 제시하는 미세 조정된 포트폴리오 투자 비중을 실제 구현하는 것을 어렵게 만든다. 특히 개인 투자자나 소규모 기관 투자자의 경우, 충분한 분산 효과를 얻기 위해 여러 부동산 자산에 투자하는 데 필요한 최소 자본 규모가 클 수 있다.
아래 표 2는 MVD의 주요 가정들과 부동산 자산의 실제 특성 간의 차이점을 요약하고, 이로 인해 발생하는 MVD 적용의 어려움을 보여준다.
표 2: MVD 가정 vs. 부동산 자산 특성
| MVD 가정 | 부동산 자산 특성 | MVD 적용의 어려움 |
|---|---|---|
| 유동성 | 높음 / 마찰 없음 | 낮음 / 비유동적 |
| 거래 비용 | 0 | 높음 |
| 자산 분할 가능성 | 완전 분할 가능 | 불가분성 / 덩어리짐 |
| 자산 동질성 | 자산군 내 동질성 가정 | 매우 이질적 |
| 정보 | 완전 / 대칭 | 불완전 / 비대칭 |
이 표는 부동산 자산 자체의 물리적, 시장적 특성이 MVD가 상정하는 이상적인 시장 조건과 어떻게 다른지를 명확히 보여준다. 이는 표 1(수익률 분포 문제)과 함께, 왜 유동적이고 표준화된 마찰 없는 시장을 위해 설계된 모델을 복잡하고 비유동적인 부동산 자산군에 적용하는 것이 근본적으로 문제가 되는지를 구조적으로 설명한다.
4.4. 추정의 어려움과 주관성 개입
MVD의 실용성은 입력 변수(기대수익률, 분산, 공분산) 추정의 정확성에 크게 좌우되지만, 부동산 자산의 경우 이러한 추정 과정 자체가 매우 어렵고 주관성이 개입될 여지가 많다.
4.4.1. 입력 변수 추정의 어려움
이질적이고 비유동적인 부동산 자산에 대해 신뢰할 수 있는 기대수익률, 분산, 공분산을 추정하는 것은 매우 어려운 과제이다. 과거 데이터는 부족하거나 감정평가 기반 데이터의 평활화 문제 등으로 인해 왜곡되어 있을 수 있다. 미래 예측은 본질적으로 불확실하며, 특히 부동산 시장의 국지성과 경기 민감성을 고려할 때 더욱 어렵다.
결정적으로 MVD의 최적화 결과(예: 최적 포트폴리오 가중치)는 이러한 입력값 추정치에 매우 민감하게 반응한다. 입력값에 작은 오류가 포함되더라도 완전히 다른, 심지어 비합리적인 포트폴리오 배분 결과를 초래할 수 있다.
4.4.2. 모수 선택 및 위험 평가의 주관성
데이터 부족과 추정의 어려움은 필연적으로 분석가의 주관적인 판단 개입을 증가시킨다. 예를 들어, 과거 데이터 사용 기간을 어떻게 설정할 것인지, 미래 시장 상황을 어떻게 예측하여 기대수익률을 조정할 것인지, 비유동성이나 법적 위험과 같은 정량화하기 어려운 위험에 대해 어느 정도의 위험 프리미엄(risk premium)을 적용할 것인지 등은 분석가의 주관적인 판단에 크게 의존하게 된다. 위험조정할인율을 결정할 때 위험할증률을 얼마로 설정할 것인가에 대한 주관성 개입 가능성이 높다는 점이 지적된다. 결과적으로 동일한 MVD 프레임워크를 사용하더라도 분석가마다 다른 주관적인 가정과 판단을 적용하여 상이한 결론에 도달할 수 있다.
부동산 자산의 고유한 특성과 MVD 입력 변수 추정의 내재적 어려움이 결합될 때, '쓰레기 입력, 쓰레기 출력(Garbage In, Garbage Out)'의 위험이 커진다. MVD는 정량적 모델로서 정확한 입력값을 요구하지만, 부동산 관련 데이터는 종종 불완전하고, 평활화되어 있으며, 이질성으로 인해 추정 오차가 크다. 이렇게 잠재적으로 결함이 있는 데이터를 민감한 최적화 모델에 입력하면, 수학적으로는 최적화된 것처럼 보이지만 실제로는 의미가 없거나 위험한 결과를 초래할 수 있다. 이는 부동산 맥락에서 MVD 결과를 맹목적으로 수용하기보다는 비판적으로 평가해야 할 필요성을 강조한다.
5. 평균-분산 분석을 넘어서: 대안적 및 보완적 접근법
평균-분산 결정법(MVD)의 한계, 특히 부동산 투자 분석에서의 한계를 인식하면서, 투자 분석가들과 연구자들은 이를 보완하거나 대체할 수 있는 다양한 접근법들을 모색해왔다. 이러한 방법들은 MVD가 간과하는 위험의 측면을 포착하거나, 보다 현실적인 가정에 기반하여 투자 결정을 지원하는 것을 목표로 한다.
5.1. 상대적 위험 평가를 위한 변동계수(Coefficient of Variation, CV) 활용
변동계수(CV)는 투자의 위험(표준편차)을 기대수익률로 나눈 값으로 정의된다. 즉, CV = 표준편차 / 기대수익률 이다.
CV의 주요 장점은 기대수익률 단위당 위험도를 측정한다는 점이다. 이는 기대수익률과 위험 수준이 모두 다른 투자 대안들을 비교할 때 유용하다. MVD의 지배원리는 한 투자안이 다른 투자안보다 기대수익률과 위험이 모두 높거나 모두 낮을 경우 명확한 우열을 가리기 어려울 수 있는데, CV는 이러한 상황에서 상대적인 위험 효율성을 비교하는 기준을 제공할 수 있다. 일반적으로 변동계수가 낮을수록 기대수익률 단위당 감수해야 하는 위험이 적다는 의미이므로, 더 효율적인 투자안으로 간주된다.
그러나 변동계수 역시 위험 측정 지표로 표준편차를 사용하므로, 수익률 분포의 비정규성 문제나 표준편차가 부동산의 모든 위험을 포착하지 못하는 근본적인 한계에서 자유롭지 못하다.
5.2. 불확실성 모델링을 위한 시나리오 분석(Scenario Analysis)
시나리오 분석은 미래에 발생 가능한 여러 가지 구체적인 상황(시나리오)들을 설정하고, 각 시나리오 하에서 투자의 성과(예: 수익률, 현금흐름, 가치)가 어떻게 변화하는지를 평가하는 방법이다. 일반적으로 낙관적(best-case), 비관적(worst-case), 그리고 가장 가능성이 높은 기본(base-case) 시나리오 등을 설정하여 분석한다.
시나리오 분석의 장점은 MVD와 같은 순수 통계적 접근법을 넘어서, 특정 거시경제적 사건(예: 금리 급등, 경기 침체), 시장 변화(예: 경쟁 심화, 공급 과잉), 또는 특정 부동산 관련 사건(예: 주요 임차인 이탈, 예상치 못한 대규모 수선 발생)이 투자 성과에 미치는 구체적인 영향을 평가할 수 있다는 점이다. 이를 통해 투자자는 발생 가능한 다양한 결과의 범위를 파악하고, 특히 부정적인 시나리오 하에서의 잠재적 손실 규모를 가늠하여 위험 관리 전략을 수립할 수 있다.
하지만 시나리오 분석은 어떤 시나리오를 포함할지, 각 시나리오의 발생 확률을 어떻게 설정할지 등에 분석가의 주관적인 판단이 개입될 여지가 크다는 단점이 있다.
5.3. 기타 위험 측정 지표 및 모델 개관
MVD의 한계를 보완하기 위해 다양한 대안적 위험 측정 지표와 모델들이 제안되었다.
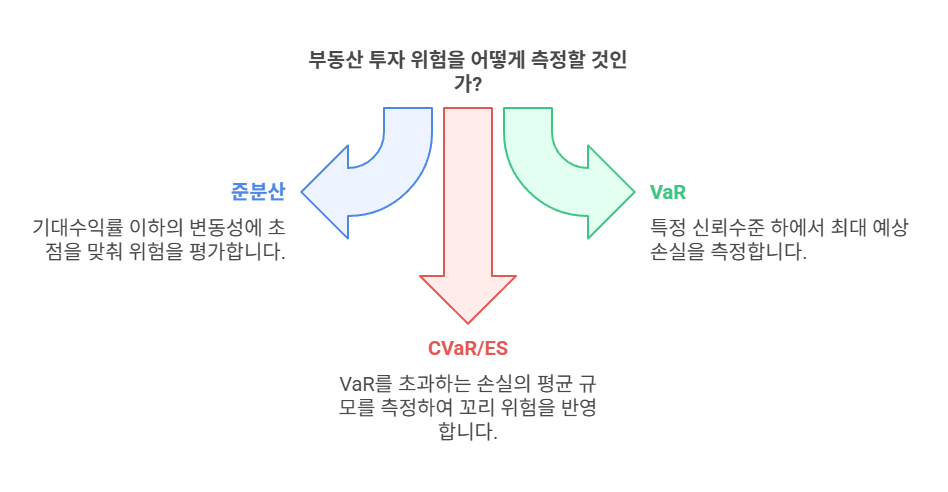
- 하방 위험 측정 지표(Downside Risk Measures): 투자자들이 손실 가능성에 더 민감하다는 점에 착안하여, 전체 변동성이 아닌 하방 변동성에 초점을 맞춘 지표들이다.
- 준분산(Semi-variance): 기대수익률 또는 목표수익률 이하의 수익률 변동성만을 측정하여 위험을 평가한다.
- VaR(Value-at-Risk): 주어진 신뢰수준 하에서 특정 기간 동안 발생할 수 있는 최대 예상 손실 금액을 측정한다.
- CVaR(Conditional Value-at-Risk) 또는 ES(Expected Shortfall): VaR 수준을 초과하는 손실이 발생했을 경우의 평균적인 손실 규모를 측정하여, 꼬리 위험(tail risk)을 보다 잘 반영한다.
- 수정된 MVD 또는 확장 모델: MVD의 가정을 완화하거나 확장하려는 시도들도 있다.
- 고차 모멘트(Higher Moments) 고려: 평균과 분산뿐만 아니라, 수익률 분포의 왜도(skewness)나 첨도(kurtosis)까지 고려하여 포트폴리오를 최적화하는 모델들이 연구되었다.
- 강건한 추정(Robust Estimation) 기법: 입력 변수 추정 오류의 영향을 줄이기 위해 통계적으로 보다 안정적인 추정 방법을 사용하거나(예: 축소 추정량(Shrinkage estimators)), 베이즈 정리(Bayesian techniques)를 활용하는 접근법도 있다.
- 기타 투자 분석 도구: MVD는 포트폴리오 배분 관점의 분석 도구이지만, 개별 투자 프로젝트의 타당성을 평가하는 데는 다른 기법들이 함께 사용되는 경우가 많다.
- 할인현금흐름(Discounted Cash Flow, DCF) 분석: 순현재가치(Net Present Value, NPV), 내부수익률(Internal Rate of Return, IRR) 등은 미래 예상 현금흐름을 현재가치로 할인하여 투자의 경제성을 평가하는 대표적인 방법이다. NPV는 투자로 인해 창출되는 절대적인 가치 증가분을 보여주며, 일반적으로 상호 배타적인 투자안 비교 시 IRR보다 우월한 기준으로 간주된다. IRR은 투자의 수익률을 비율로 나타내지만, 재투자율 가정 문제나 복수 해(multiple IRR) 문제 등의 단점이 있다.
- 수정내부수익률(Modified IRR, MIRR) 및 XIRR: IRR의 재투자율 가정 문제를 완화하거나, 비정기적인 현금흐름에 대한 수익률을 계산하기 위해 사용된다.
- 회수기간법(Payback Period, PP): 초기 투자 비용을 회수하는 데 걸리는 기간을 측정하는 간단한 방법이지만, 화폐의 시간가치와 회수기간 이후의 현금흐름을 무시한다는 단점이 있다.
아래 표 3은 MVD를 보완하거나 대체할 수 있는 주요 접근법들의 핵심 개념과 장단점을 요약한 것이다.
표 3: MVD 대안적/보완적 접근법 요약
| 접근법 | 핵심 개념 | MVD 대비 장점 | 한계점 |
|---|---|---|---|
| 변동계수 (CV) | 수익률 단위당 위험도 | MVD로 비교 어려운 자산 비교 가능 | 여전히 분산 사용, 비정규성 문제 미해결 |
| 시나리오 분석 | 미래 상황별 성과 평가 | 특정 사건, 비통계적 위험 모델링 가능 | 시나리오/확률 설정 주관성 |
| 하방 위험 측정 (VaR, CVaR, 준분산) |
잠재적 손실 규모/확률 측정 | 손실 회피 성향 더 잘 반영 | 계산 복잡성, 데이터 요구량 많음 |
| 강건한 추정 / 수정된 MVD | 입력값 오류 감소, 고차 모멘트 고려 | 추정 오류, 비정규성 문제 완화 시도 | 수학적 복잡성 증가 |
| NPV / IRR / MIRR / PP | 프로젝트 현금흐름 기반 타당성 분석 | 상세한 개별 프로젝트 경제성 평가 | 직접적인 포트폴리오 최적화 도구는 아님 |
이 표는 MVD의 한계를 극복하기 위한 다양한 방법론들을 개괄적으로 보여준다. 각 접근법은 MVD가 놓치는 부분을 보완하려는 시도이지만, 동시에 자체적인 한계점도 가지고 있다. 따라서 부동산 투자 분석 실무에서는 특정 방법론에만 의존하기보다는, 분석 목적과 데이터 가용성, 투자자의 위험 선호도 등을 종합적으로 고려하여 여러 기법들을 상호 보완적으로 활용하는 것이 바람직하다.
6. 결론: 부동산 투자 분석에서의 실질적 시사점
평균-분산 결정법(MVD)은 자산 배분 및 포트폴리오 관리 분야에서 이론적 토대를 제공하며, 특히 분산투자를 통한 위험 관리와 위험-수익 간의 상충관계를 이해하는 데 중요한 기여를 했다. 수학적 명료성과 상대적 단순성 덕분에 MVD는 금융 교육 및 연구에서 여전히 중요한 위치를 차지하고 있다.
그러나 MVD를 실제 투자, 특히 부동산 투자 영역에 직접 적용하는 데에는 심각한 한계와 잠재적 오류가 존재한다. 본 보고서에서 상세히 분석했듯이, 부동산 자산의 고유한 특성들은 MVD의 핵심 가정들과 충돌하는 경우가 많다. 주요 한계점들을 요약하면 다음과 같다:
- 수익률 분포 문제: 부동산 수익률은 종종 정규분포 가정을 위배하며(왜도, 팻 테일), 감정평가 기반 데이터는 평활화되어 실제 변동성과 상관관계를 왜곡시킨다.
- 위험 측정의 한계: 분산/표준편차는 부동산의 다면적 위험(특히 하방 위험, 유동성 위험, 운영 위험, 법률/규제 위험 등)을 충분히 포착하지 못한다.
- 부동산 특성 반영의 어려움: 비유동성, 높은 거래 비용, 자산의 이질성, 정보 비대칭성, 불가분성 등 부동산 고유의 특성들은 MVD 모델 적용을 어렵게 만든다.
- 입력 변수 추정의 난점: 기대수익률, 분산, 공분산 등 MVD의 핵심 입력 변수를 부동산 자산에 대해 정확하게 추정하는 것이 매우 어렵고, 추정 오류는 결과의 신뢰성을 크게 저하시킨다. 또한, 추정 과정에 분석가의 주관성이 개입될 여지가 많다.
이러한 한계점들을 고려할 때, 부동산 투자 분석 및 포트폴리오 구성 실무에서 MVD를 활용하고자 하는 전문가들에게는 다음과 같은 접근 방식이 권장된다:
- MVD를 맹신하지 말고 비판적으로 활용하라: MVD는 위험-수익 관계를 이해하는 출발점은 될 수 있지만, 부동산 포트폴리오 배분을 위한 최종적이고 유일한 해답으로 간주해서는 안 된다. MVD 결과는 항상 현실적인 제약과 모델의 한계를 염두에 두고 해석해야 한다.
- 입력 데이터의 질을 개선하고 조정하라: 가능하다면 감정평가 데이터의 평활화 효과를 보정하려는 시도(de-smoothing)를 하거나, 과거 데이터뿐만 아니라 미래 예측 및 시장 전망을 반영하여 기대수익률과 위험 추정치를 조정해야 한다. 특히, 비유동성 프리미엄이나 특정 법률/규제 위험 등 MVD가 직접 포착하지 못하는 위험 요인에 대한 주관적 판단을 위험 프리미엄 형태로 반영하는 것을 고려해야 한다.
- 강건한(Robust) 추정 기법 및 대안 모델을 고려하라: 데이터의 불확실성과 비정규성 문제에 보다 잘 대응할 수 있도록 설계된 통계적 기법이나, MVD의 가정을 완화한 모델(예: 하방 위험 기반 모델)의 적용 가능성을 검토할 수 있다.
- 정량적 분석과 정성적 분석을 결합하라: MVD와 같은 정량적 모델 분석 결과는 반드시 심층적인 정성적 분석과 결합되어야 한다. 개별 부동산의 입지, 물리적 상태, 임차인 구성, 시장 경쟁 환경, 법적 제약 조건 등에 대한 철저한 실사(due diligence)와 전문가적 판단이 필수적이다. 시나리오 분석과 같은 기법을 활용하여 다양한 잠재적 위험 요인의 영향을 평가하는 것도 중요하다.
- 장기적 관점을 유지하고 빈번한 리밸런싱을 지양하라: 부동산 투자는 본질적으로 장기적인 관점에서 접근해야 하며, 높은 거래 비용과 비유동성을 고려할 때 MVD 결과에 따른 단기적이고 빈번한 포트폴리오 조정은 비현실적일 뿐만 아니라 비용 비효율적일 수 있다. 전략적인 자산 배분 결정에 초점을 맞추어야 한다.
결론적으로, 평균-분산 결정법은 포트폴리오 이론의 중요한 개념적 틀을 제공하지만, 복잡하고 독특한 특성을 지닌 부동산 투자 세계에 적용하기에는 상당한 주의와 비판적 시각, 그리고 보완적인 분석 도구의 활용이 요구된다. 수학적 정교함에 매몰되기보다는 현실적인 제약과 다양한 위험 요인을 종합적으로 고려하는 균형 잡힌 접근 방식이 성공적인 부동산 투자 의사결정의 핵심이라 할 수 있다.
[부동산] 부동산 주요개념 총정리
부동산에 대한 개념을 이해하기 쉽게 올리고 있습니다. 올해는 여러분 모두 성공적인 한 해가 되시길 기원하는 마음으로 작성하였습니다. 부동산총론부동산의 기본 개념, 정의, 관련 제도를
jkcb.tistory.com
본 문서에 포함된 부동산 관련 정보는 일반적인 참고와 이해를 돕기 위한 목적으로 작성되었습니다. 포함되는 내용은 법률, 세무, 부동산 거래, 또는 기타 전문적인 조언을 대체하지 않으며, 특정 상황에 대한 법적 효력이나 권고를 보장하지 않습니다.
본 정보를 활용하여 발생하는 모든 결정, 행동, 또는 그로 인한 결과 (재정적 손실, 법적 분쟁 등 포함) 에 대해 작성자는 어떠한 책임도 지지 않습니다. 부동산 관련 거래나 의사결정을 진행하기 전, 반드시 해당 분야의 전문가 (변호사, 공인중개사, 세무사) 와 상담하시기 바랍니다.
또한, 본 문서에 포함된 정보는 작성 시점에서의 자료를 기반으로 하며, 이후 법률, 규제, 시장 상황 등의 변경으로 인해 최신 정보와 다를 수 있습니다. 사용자는 본 정보를 활용하기 전 최신 정보를 확인할 책임이 있습니다.