딥러닝에서 미분이란? 인공신경망의 편도함수와 미분의 특징

인공 신경망 분야에서 미분은 학습 과정에서 사용되는 기본 개념이며, 입력에 대한 함수의 변화율을 계산하는 방법입니다.

목차

 

경사하강법

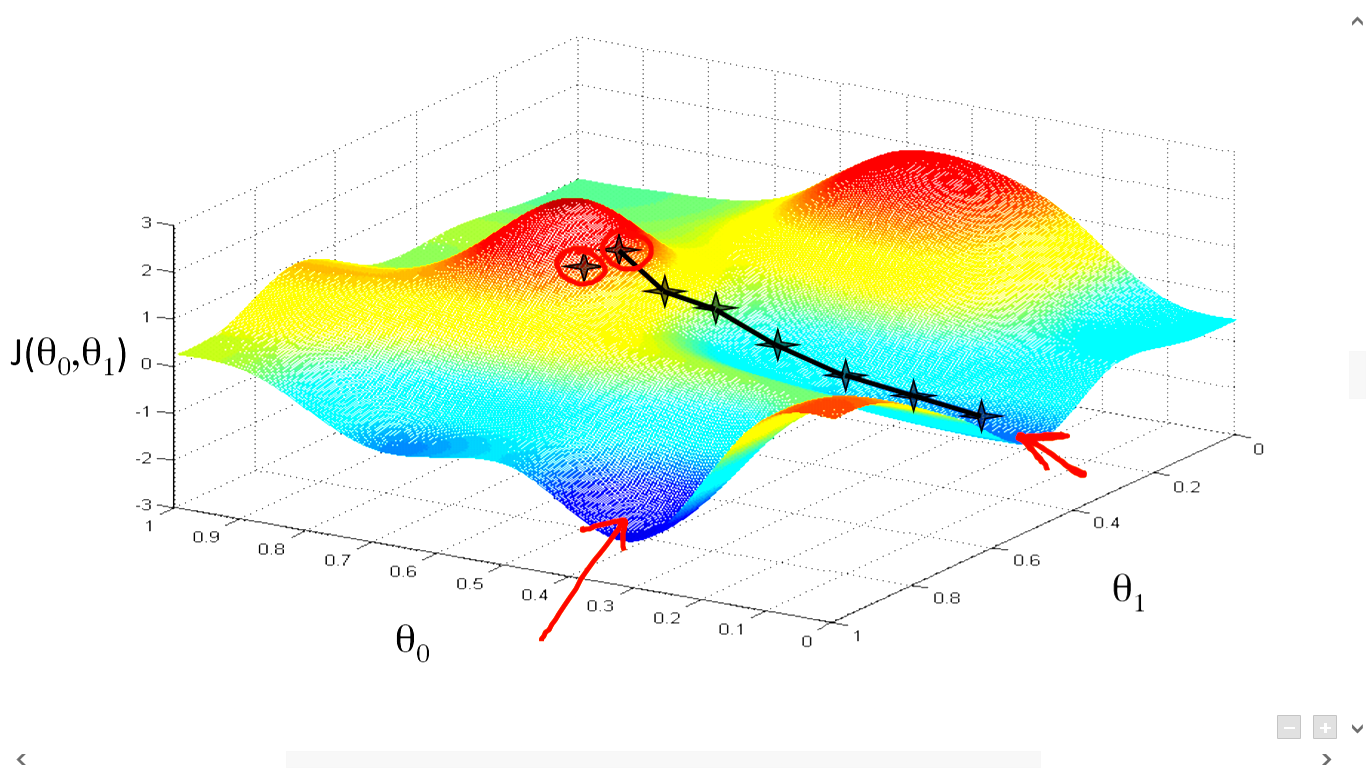
딥러닝에서 미분이란

신경망 훈련 과정에는 모델의 매개변수를 조정하여 손실 함수 값을 최소화하는 과정이 포함됩니다. 손실 함수는 예측 출력과 실제 출력의 차이를 측정하는 수학 함수입니다. 매개변수를 조정하려면 매개변수에 대한 손실 함수의 기울기를 계산해야 합니다.

그래디언트는 함수 값의 가장 가파른 증가 방향을 가리키는 벡터입니다. 기울기의 반대는 가장 가파른 감소 방향입니다. 손실 함수를 최소화하기 위해 매개변수를 조정하는 과정을 경사 하강법이라고 합니다.

그래디언트를 계산하는 과정을 역전파라고 합니다. 복잡한 함수의 그래디언트를 계산하기 위한 계산상 효율적인 방법입니다. 역전파는 신경망의 최종 출력에서 시작하여 계층을 통해 역방향으로 작동하여 각 매개변수에 대한 손실 함수의 기울기를 계산합니다.

요약하면, 미분은 인공 신경망 분야의 기본 개념입니다. 입력에 대한 함수의 변화율을 계산하기 위해 훈련 과정에서 사용됩니다. 매개변수에 대한 손실함수의 기울기를 계산하여 모델의 매개변수를 조정하고 손실함수의 값을 최소화해야 합니다. 이 프로세스를 경사하강법이라고 하며 경사를 계산하는 데 사용되는 방법을 역전파라고 합니다.

편도함수와 미분

인공 신경망(ANN) 분야에서 부분 도함수는 신경망의 훈련 과정에서 중요한 역할을 합니다. 개별 뉴런의 가중치 및 편향과 관련하여 네트워크의 출력이 얼마나 변경되는지 측정하는 데 사용됩니다.

ANN을 교육할 때 목표는 예측된 출력과 원하는 출력 사이의 오류를 최소화하는 것입니다. 이를 달성하기 위해서는 뉴런의 가중치와 편향을 조정해야 합니다. 각 가중치 및 편향에 대한 오차의 편도함수는 특정 가중치 또는 편향을 조정하면 오차가 얼마나 변경되는지 알려줍니다. 이 정보를 사용하여 전체 오류를 줄이고 네트워크 성능을 향상시키는 방식으로 가중치와 편향을 조정할 수 있습니다.

편도함수를 기반으로 가중치와 편향을 조정하는 프로세스를 역전파라고 합니다. 네트워크의 각 가중치와 편향에 대해 편도함수를 계산한 다음 이를 조정하는 데 사용하는 반복 프로세스입니다. 가중치와 편향이 조정되면 오류가 줄어들고 네트워크 성능이 향상됩니다.

요약하면 편도함수는 ANN 훈련을 위한 강력한 도구입니다. 이를 통해 개별 뉴런의 가중치 및 편향과 관련하여 네트워크 출력이 얼마나 변경되는지 측정할 수 있습니다. 이 정보를 사용하여 전체 오류를 줄이고 네트워크 성능을 향상시키는 방식으로 가중치와 편향을 조정할 수 있습니다. 편도함수를 이해하고 활용하는 것은 ANN의 성능을 훈련하고 최적화하는 데 필수적입니다.

신경망 기울기 구현

import numpy as np

# Define the network's architecture
input_size = 2
hidden_size = 3
output_size = 1

# Initialize the weights and biases
weights = {
    'hidden': np.random.randn(input_size, hidden_size),
    'output': np.random.randn(hidden_size, output_size)
}
biases = {
    'hidden': np.random.randn(hidden_size),
    'output': np.random.randn(output_size)
}

# Define the activation function (sigmoid in this example)
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

# Define the forward pass of the network
def forward(x, weights, biases):
    hidden_layer = np.dot(x, weights['hidden']) + biases['hidden']
    hidden_layer_output = sigmoid(hidden_layer)
    output_layer = np.dot(hidden_layer_output, weights['output']) + biases['output']
    output = sigmoid(output_layer)
    return output

# Define the backward pass (backpropagation)
def backward(x, y, weights, biases, output):
    # Calculate the error
    error = y - output

    # Calculate the gradient for the output layer
    output_layer_error = error * output * (1 - output)
    output_layer_gradient = np.dot(hidden_layer_output.T, output_layer_error)

    # Calculate the gradient for the hidden layer
    hidden_layer_error = np.dot(output_layer_error, weights['output'].T) * hidden_layer_output * (1 - hidden_layer_output)
    hidden_layer_gradient = np.dot(x.T, hidden_layer_error)

    # Return the gradients
    return {
        'hidden': hidden_layer_gradient,
        'output': output_layer_gradient
    }

# Define the training data
x = np.array([[1, 2], [2, 3], [3, 4]])
y = np.array([[0], [0], [1]])

# Perform the forward and backward pass
output = forward(x, weights, biases)
gradients = backward(x, y, weights, biases, output)

# Update the weights and biases based on the gradients
learning_rate = 0.1
weights['hidden'] += learning_rate * gradients['hidden']
weights['output'] += learning_rate * gradients['output']
biases['hidden'] += learning_rate * np.mean(gradients['hidden'], axis=0)
biases['output'] += learning_rate * np.mean(gradients['output'], axis=0)

관련 글

'컴퓨터과학/딥러닝' 카테고리의 글 목록