목차
퍼셉트론이란
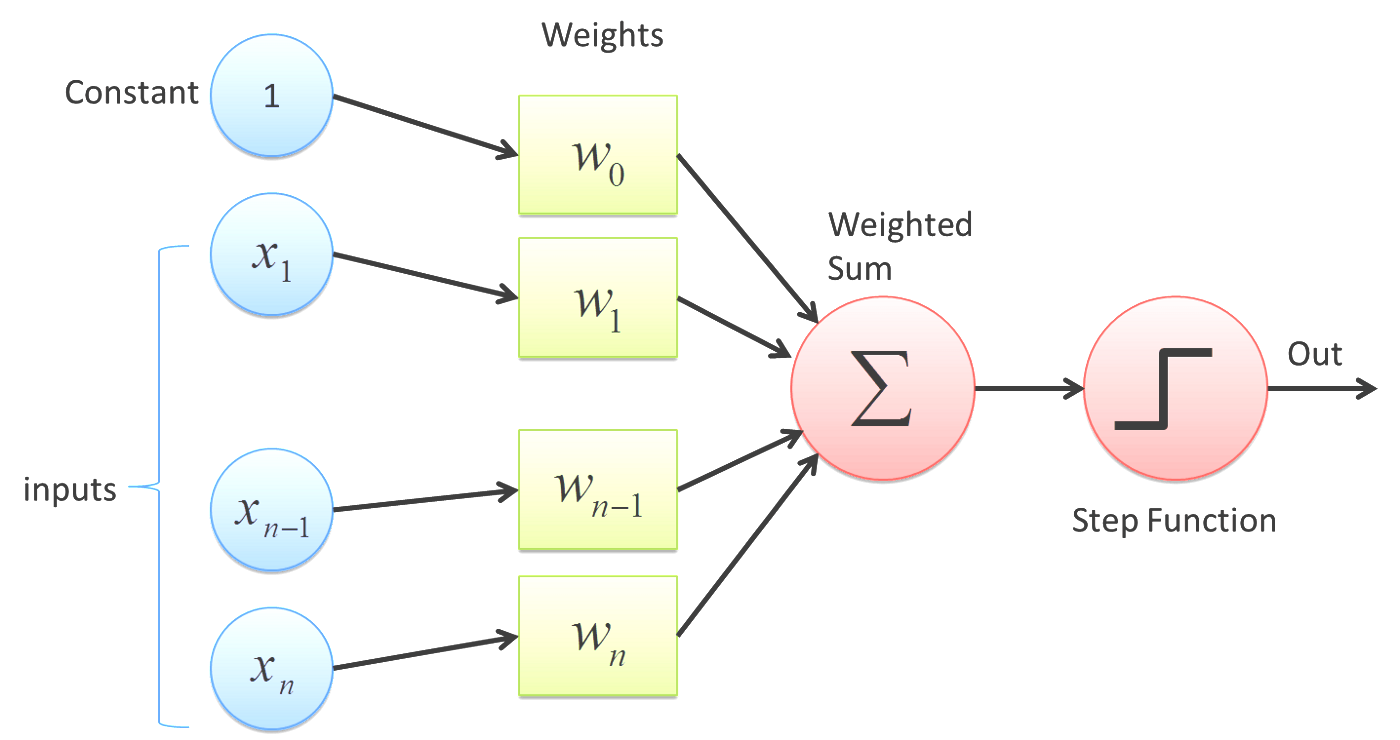
퍼셉트론은 1950년대 후반에 처음 도입된 일종의 인공 신경망(ANN)입니다. 인간의 뇌가 정보를 처리하는 방식을 모방하도록 설계된 생물학적 뉴런의 단순화된 모델입니다.
퍼셉트론은 단일 계층의 인공 뉴런으로 구성되며 각 뉴런은 일련의 가중치에 의해 입력 계층에 연결됩니다. 입력은 퍼셉트론에 공급되고 퍼셉트론은 입력과 가중치를 기반으로 출력을 생성합니다. 퍼셉트론은 활성화 함수라는 수학 함수를 사용하여 출력을 결정합니다.
퍼셉트론은 일반적으로 입력을 두 범주 중 하나로 분류하는 것이 목표인 이진 분류 문제에 사용됩니다. 퍼셉트론은 입력 데이터를 두 가지 범주로 구분하는 선형 결정 경계를 기반으로 입력 데이터를 분류하는 데 사용할 수 있습니다. 퍼셉트론은 교육이라는 프로세스를 사용하여 입력 데이터와 원하는 출력을 기반으로 입력 및 출력 레이어 간의 연결 가중치를 조정합니다.
퍼셉트론은 ANN의 기본 모델로 간주되며 기계 학습에 사용할 수 있는 최초의 알고리즘 중 하나로 간주됩니다. 영상인식, 음성인식, 자연어 처리 등의 간단한 작업에 사용할 수 있습니다. 그러나 퍼셉트론에는 선형적으로 분리 가능한 문제만 해결할 수 있고 훈련 과정 중에 로컬 최솟값에 갇힐 수 있는 것과 같은 몇 가지 제한 사항이 있다는 점에 유의하는 것이 중요합니다.
요약하자면, 퍼셉트론은 선형 결정 경계를 기반으로 입력 데이터를 두 가지 범주로 분류하는 데 사용할 수 있는 인공 신경망의 단순하고 기본적인 모델입니다.
퍼셉트론 공식
퍼셉트론 공식은 인공 신경망의 일종인 퍼셉트론의 출력을 계산하는 데 사용됩니다. 공식은 선형 결정 경계를 기반으로 입력 데이터를 두 범주 중 하나로 분류해야 하는지 여부를 결정하는 데 사용됩니다.
퍼셉트론의 기본 공식은 다음과 같습니다.
y = f(w*x + b)
y는 퍼셉트론의 출력입니다.
f(x)는 활성화 함수입니다.
w는 입력 레이어와 출력 레이어 간의 연결 강도를 나타내는 가중치 벡터입니다.
x는 입력 벡터입니다.
b는 결정 경계를 변경하기 위해 조정할 수 있는 값인 바이어스입니다.
활성화 함수(f(x))는 입력을 출력에 매핑하는 수학 함수입니다. 퍼셉트론에 일반적으로 사용되는 활성화 함수는 계단 함수, 부호 함수 및 시그모이드 함수입니다.
- 계단 함수는 임계값을 기준으로 입력을 출력에 매핑하는 간단한 함수입니다. 입력이 임계값보다 크면 출력은 1이고 그렇지 않으면 0입니다.
- 부호 함수는 계단 함수와 비슷하지만 입력 부호를 기준으로 입력을 출력에 매핑합니다. 입력이 0보다 크면 출력은 1이고 그렇지 않으면 -1입니다.
- 시그모이드 함수는 입력을 출력에 매끄럽게 매핑하부는 보다 복잡한 함수로 출력이 확률일 때 일반적으로 사용됩니다.
[컴퓨터과학/딥러닝] - 계단 함수란? 딥러닝의 계단 활성화 함수 특징과 구현방법
[컴퓨터과학/딥러닝] - 시그모이드 함수란? 딥러닝의 시그모이드 활성화 함수 구현방법
출력이 계산된 후 퍼셉트론은 출력을 원하는 출력과 비교하고 차이가 있는 경우 퍼셉트론은 차이를 줄이기 위해 가중치와 편향 값을 조정합니다. 이 과정을 훈련이라고 합니다.
요약하자면, 퍼셉트론 공식은 인공 신경망의 일종인 퍼셉트론의 출력을 계산하는 데 사용됩니다. 수식은 입력, 가중치, 편향 및 활성화 함수를 사용하여 출력을 계산하고 입력 범주에 대한 예측을 수행합니다. 퍼셉트론은 훈련 과정에서 계산된 출력과 원하는 출력 간의 차이를 기반으로 가중치와 편향을 조정합니다.
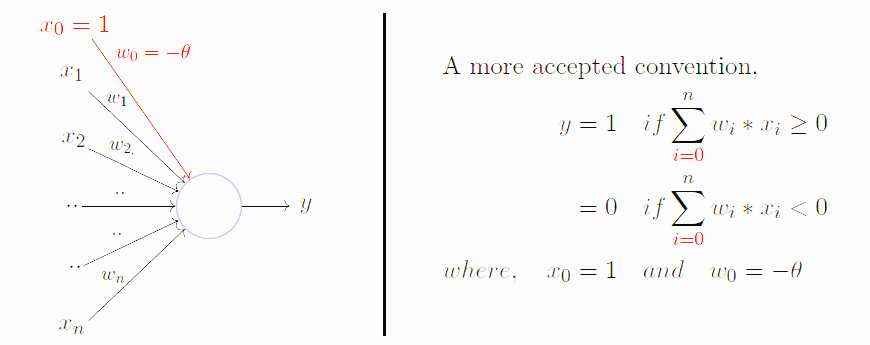
퍼셉트론 구현
import numpy as np
class Perceptron:
def __init__(self, num_inputs, activation_function):
self.weights = np.random.rand(num_inputs)
self.bias = np.random.rand(1)
self.activation_function = activation_function
def predict(self, inputs):
weighted_sum = np.dot(inputs, self.weights) + self.bias
return self.activation_function(weighted_sum)
def train(self, inputs, desired_output, learning_rate):
output = self.predict(inputs)
error = desired_output - output
self.weights += learning_rate * error * inputs
self.bias += learning_rate * error
def step_function(x):
if x >= 0:
return 1
else:
return 0
# Initialize the perceptron with 2 inputs and the step function as the activation function
perceptron = Perceptron(2, step_function)
# Inputs for the AND gate
inputs = np.array([[1, 1], [1, 0], [0, 1], [0, 0]])
# Desired outputs for the AND gate
desired_outputs = np.array([1, 0, 0, 0])
# Training the perceptron
for i in range(1000):
for inputs, desired_output in zip(inputs, desired_outputs):
perceptron.train(inputs, desired_output, 0.1
위의 코드는 Python에서 간단한 퍼셉트론을 구현하는 방법의 예입니다. 구현은 여러 부분으로 나뉩니다.
퍼셉트론 클래스: 이 클래스는 퍼셉트론의 구조를 정의하며 init, predict 및 train의 세 가지 메서드가 있습니다.
init 메소드: 이 메서드는 클래스의 인스턴스가 생성될 때 호출됩니다. 임의의 값으로 가중치와 편향을 초기화하고 입력 수와 활성화 함수를 인수로 사용합니다.
예측 방법: 이 방법은 입력을 받아 입력과 가중치의 가중 합을 계산한 다음 가중 합에 활성화 함수를 적용합니다.
학습 방법: 이 방법은 입력, 원하는 출력 및 학습률을 인수로 사용합니다. 예측 방법을 사용하여 출력을 계산하고 원하는 출력과 계산된 출력의 차이로 오류를 계산합니다. 그런 다음 오류와 학습률을 사용하여 가중치와 편향을 업데이트합니다.
step_function: 이 함수는 이 예제에서 활성화 함수로 사용되는 간단한 단계 함수입니다. 이 함수는 입력을 받아 0보다 크거나 같으면 1을 반환하고 그렇지 않으면 0을 반환합니다.
퍼셉트론이 정의된 후 활성화 함수로 2개의 입력과 step_function을 사용하여 인스턴스가 생성됩니다.
퍼셉트론의 선형과 비선형
퍼셉트론에서 결정 경계는 입력 변수와 가중치의 선형 조합으로 정의됩니다. 선형 조합은 입력 벡터와 가중치 벡터의 내적을 사용하여 계산되며 활성화 함수를 통과하여 출력을 생성합니다.
퍼셉트론의 선형성은 입력 변수와 가중치 사이의 선형 관계를 의미하며 내적으로 표현됩니다. 단계 함수 또는 부호 함수와 같은 선형 활성화 함수를 사용하는 퍼셉트론은 선형 분류기로 간주됩니다. 선형적으로 분리 가능한 문제만 해결할 수 있습니다. 즉, 입력 데이터를 하나의 직선으로 두 범주로 분리할 수 있습니다.
퍼셉트론의 비선형성은 결정 경계에 비선형성을 도입하여 퍼셉트론이 비선형적으로 분리 가능한 문제를 해결할 수 있도록 하는 시그모이드 또는 ReLU 함수와 같은 비선형 활성화 함수의 사용을 의미합니다. 이러한 함수는 퍼셉트론이 더 복잡한 데이터를 분리할 수 있도록 곡선 결정 경계를 생성할 수 있습니다.
요약하면, 퍼셉트론의 선형성은 입력 변수와 가중치 사이의 선형 관계를 의미하고, 비선형성은 비선형 활성화 함수를 사용하는 것을 의미합니다. 선형 퍼셉트론은 선형적으로 분리 가능한 문제만 풀 수 있는 반면, 비선형 퍼셉트론은 결정 경계에 비선형성을 도입하여 비선형적으로 분리 가능한 문제를 풀 수 있습니다.
'컴퓨터과학/딥러닝' 카테고리의 글 목록
모든 분야의 정보를 담고 있는 정보의 호텔입니다.
jkcb.tistory.com