계단 함수란? 딥러닝의 계단 활성화 함수 특징과 구현방법

목차

 

개요

계단 함수는 입력을 이진 출력(0 또는 1)으로 매핑하는 활성화 함수입니다. 주로 이진 분류 문제의 출력 계층에서 사용됩니다. 

단계 함수는 다음과 같이 정의됩니다.

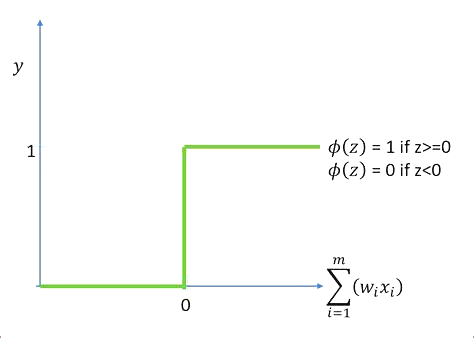
계단함수(x) = 1 if x >= 0 else 0

 

계단 함수 그래프

 

특징

계단 함수는 실수에 대해서만 정의되며 입력이 0보다 크거나 같으면 1, 입력이 0보다 작으면 0인 출력을 생성합니다. 단계 함수는 연속적으로 미분할 수 없으므로 최적화 프로세스를 만들 수 있습니다. 특히 네트워크에 여러 계층이 있는 경우 더 어렵습니다.

계단 함수는 모델이 출력에 대해 어려운 예측을 할 수 있도록 해주기 때문에 이진 분류 문제에 유용합니다. 입력이 특정 클래스에 속하는지 여부만 나타내는 이진 출력을 생성합니다.

계단 함수는 지속적으로 미분할 수 없고 최적화를 더 어렵게 만들 수 있기 때문에 신경망에서 활성화 함수로 일반적으로 사용되지 않는다는 점은 주목할 가치가 있습니다. 또한 확률적 출력을 생성하지 않으며 불확실성을 처리하는 데 도움이 되지 않습니다. 이러한 이유로 대부분의 경우 시그모이드 또는 ReLU와 같은 다른 활성화 기능이 선호됩니다.

 

[컴퓨터과학/딥러닝] - ReLU함수란 무엇인가? ReLU 활성화 함수 특징과 구현방법

[컴퓨터과학/딥러닝] - 시그모이드 함수란? 딥러닝의 시그모이드 활성화 함수 구현방법

 

구현

다음은 Python에서 단계 함수를 구현하는 방법의 예입니다.

 

def step(x):
    if x >= 0:
        return 1
    else:
        return 0

 

이 함수는 단일 입력 x를 사용하고 여기에 단계 함수를 적용합니다. 이 함수를 사용하여 이진 분류 신경망의 출력에서 단일 뉴런 또는 전체 계층의 출력을 계산할 수 있습니다.

또한 numpy와 같은 미리 빌드된 라이브러리를 사용하여 보다 효율적이고 편리하게 단계 기능을 구현할 수 있습니다. 다음은 numpy를 사용하여 단계 함수를 구현하는 방법의 예입니다.

 

import numpy as np

def step(x):
    return np.heaviside(x, 1)

 

이 함수는 또한 입력의 단계를 반환하지만 이제 numpy 배열을 입력으로 전달할 수도 있으며 함수는 요소별로 단계를 배열의 모든 요소에 적용합니다.

 

시그모이드 함수와 계단함수 비교

시그모이드 및 계단 함수는 둘 다 신경망에서 사용되는 활성화 함수이지만 몇 가지 중요한 차이점이 있습니다.

1. 출력 범위: 시그모이드 함수는 입력을 0과 1 사이의 값에 매핑하고 계단 함수는 입력을 이진 출력(0 또는 1)에 매핑합니다. 따라서 회귀와 같은 연속 출력 문제에 시그모이드 함수가 더 적합하고 이진 분류 문제에는 단계 함수가 더 적합합니다.
   
   
2. 미분 가능성: 시그모이드 함수는 지속적으로 미분 가능합니다. 즉, 모든 점에서 도함수가 있음을 의미합니다. 이렇게 하면 역전파와 같은 기술을 사용하여 훈련 중에 네트워크의 매개변수를 더 쉽게 최적화할 수 있습니다. 반면 계단 함수는 연속적으로 미분할 수 없으므로 최적화 프로세스를 더 어렵게 만들 수 있습니다.
   
   
3. Vanishing Gradients: 학습 과정에서 네트워크의 가중치가 업데이트되면 가중치에 대한 오차의 기울기가 계산됩니다. 심층 신경망에서 활성화 함수에 대한 입력이 크면(양수 또는 음수) 기울기가 매우 작아질 수 있으며, 이를 기울기 소실이라고 합니다. 시그모이드 활성화는 이 문제로 인해 훈련 프로세스를 느리고 불안정하게 만듭니다. 반면에 단계 함수에는 이러한 문제가 없습니다.
   
   
4. 해석 가능성: 시그모이드 함수는 0과 1 사이의 출력을 생성하며, 이는 입력이 특정 클래스에 속할 확률로 해석될 수 있으므로 다중 클래스 분류 문제에 유용합니다. 반면에 계단 함수는 입력이 특정 클래스에 속하는지 여부만 나타내는 이진 출력을 생성합니다.

요약하면 시그모이드 함수는 연속 출력 문제에 더 적합하고 계단 함수는 이진 분류 문제에 더 적합합니다. 또한 시그모이드 함수는 지속적으로 미분 가능하며 최적화 프로세스에 도움이 될 수 있지만 기울기 소실 문제도 있습니다. 단계 함수에는 이 문제가 없지만 지속적으로 미분할 수 없으며 최적화를 더 어렵게 만들 수 있습니다.

 

참고

'컴퓨터과학/딥러닝' 카테고리의 글 목록