목차
소프트맥스 함수 개요
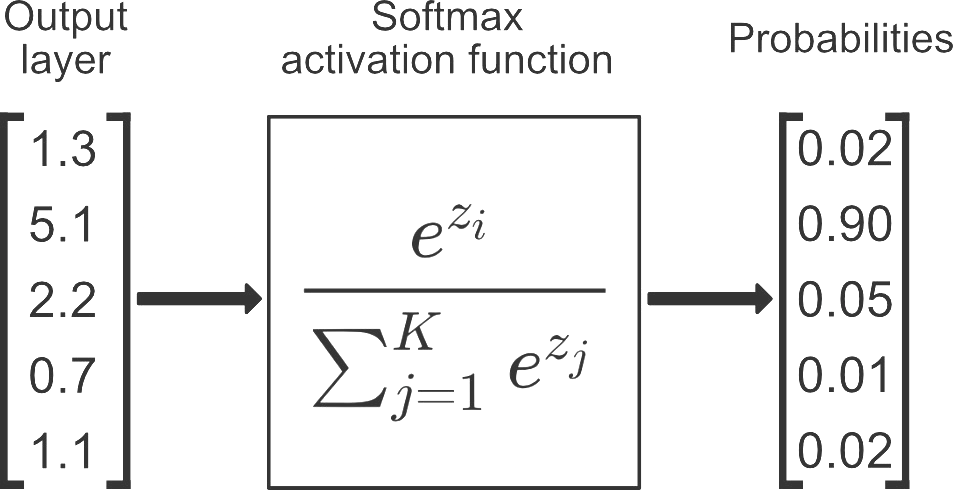
softargmax 또는 정규화된 지수 함수라고도 하는 softmax 함수는 문제가 다중 클래스 분류인 경우 신경망의 출력 계층에서 일반적으로 사용되는 활성화 함수입니다. 입력 값(실수일 수 있음)을 K 클래스에 대한 확률 분포로 매핑합니다. 여기서 K는 클래스 수입니다. 함수는 다음과 같이 정의됩니다.
softmax(x) = exp(x) / sum(exp(x))
여기서 x는 각 클래스에 대한 입력 값의 벡터이고 exp는 지수 함수이며 분모는 모든 클래스에 대한 지수 값의 합입니다.
softmax 함수의 출력은 모든 클래스에 대한 값의 합이 1인 확률 분포입니다. 이는 softmax 함수의 출력이 각 클래스에 속하는 입력의 확률로 해석될 수 있음을 의미합니다. 확률이 가장 높은 클래스가 모델의 최종 출력 또는 예측으로 선택됩니다.
softmax 함수의 주요 기능 중 하나는 출력 값을 확률로 해석할 수 있는 방식으로 정규화하여 여러 클래스를 처리할 수 있다는 것입니다. 또한 입력의 지수를 계산하므로 값이 큰 입력을 처리할 수 있으므로 언더플로 또는 오버플로의 가능성을 줄일 수 있습니다.
softmax 함수는 다중 클래스 분류, SVM, Gumbel-Softmax, Hinge loss 등과 같은 다른 대체 활성화 함수에 사용되는 유일한 활성화 함수가 아니라는 점에 유의해야 합니다.
소프트맥스 함수 구현
import numpy as np
def softmax(x):
# subtracting max for numerical stability
x -= np.max(x)
return np.exp(x) / np.sum(np.exp(x))이 예에서 함수는 입력 값 x의 벡터를 취하고 수치적 안정성을 위해 각 요소에서 x의 최대값을 뺍니다. 그런 다음 x의 각 요소에 대한 지수를 계산하고 지수의 합으로 나누어 softmax 값을 얻습니다.
다음과 같이 numpy 내장 함수를 사용하여 softmax를 계산할 수도 있습니다.
def softmax(x):
return np.exp(x) / np.sum(np.exp(x))
위의 예에서 숫자 안정성에 사용되는 x의 최대값을 빼지 않았습니다. numpy가 이미 내부적으로 처리하고 있기 때문입니다.
softmax 함수를 사용하여 주어진 입력 벡터에 대한 softmax 값을 계산할 수 있습니다.
>>> x = np.array([1, 2, 3])
>>> softmax(x)
array([0.09003057, 0.24472847, 0.66524096])
이 예에서 출력 값의 합은 1이며 이는 softmax 함수가 확률 분포를 생성했음을 확인합니다.
softmax 함수는 다중 클래스 분류를 위한 것이며 이진 분류에는 적합하지 않습니다.
이 경우 시그모이드 함수가 더 나은 선택이 될 것입니다.
장단점
장점
- softmax 함수는 확률로 해석할 수 있는 방식으로 출력 값을 정규화하여 여러 클래스를 처리할 수 있습니다.
- 입력의 지수를 계산하므로 값이 큰 입력을 처리할 수 있으므로 언더플로 또는 오버플로의 가능성을 줄일 수 있습니다.
- 미분 가능하므로 모델이 경사 하강법을 통해 학습할 수 있습니다.
- 다중 클래스 분류 문제에서 최종 활성화 함수로 사용할 수 있습니다.
- CNN(Convolutional Neural Networks) 및 RNN(Recurrent Neural Networks)과 같은 다양한 신경망 아키텍처에서 널리 사용됩니다.
단점
- 큰 입력값에 대해 softmax 함수를 평가하려면 지수와 합계를 계산해야 하므로계산 비용이 많이 들 수 있습니다.
- softmax 함수는 입력 값에 민감할 수 있으므로 입력 값의 작은 변화가 출력 값의 큰 변화로 이어질 수 있습니다.
- 모델의 성능에 부정적인 영향을 미칠 수 있는 이상값과 노이즈에 민감할 수 있습니다.
- 이진 분류에는 적합하지 않습니다.이 경우 시그모이드 함수가 더 나은 선택입니다.