목차
인공지능과 기계학습 분야에서, 탐색 알고리즘은 문제 해결에 널리 사용되는 핵심 기술 중 하나입니다. 이들 알고리즘은 다양한 분야에서 응용되며, 사용자가 원하는 목표를 달성하거나 관련 정보를 찾는 데 도움을 줍니다. 대표적으로 경로 탐색, 게임 인공지능, 자원 배치 및 최적화 문제 등에 활용되고 있습니다.
이 블로그 글에서는 인공지능에서 널리 사용되는 탐색 알고리즘 중 세 가지 - Greedy(탐욕) 알고리즘, Uniform Cost(균일 비용) 알고리즘, 그리고 A* 알고리즘에 대해 소개하고, 이들의 주요 특징과 성능을 비교해 보겠습니다. 이를 통해 독자들이 자신의 문제 해결에 가장 적합한 알고리즘을 선택하는 데 도움이 되길 바랍니다.
| 알고리즘 | 기본 개념 | 장점 | 단점 |
| Greedy | 매 단계에서 최적 선택을 하는 탐색 알고리즘 | 계산 속도가 빠르며 구현이 쉽고, 합리적인 해를 빠르게 찾을 수 있음 |
전체적인 최적해를 찾지 못할 때가 많음, 지역 최적해에 빠진 상태에서 빠져나지 못할 때가 있음
|
| Uniform Cost | 경로의 발생하는 비용을 동일하게 취급하는색 알고리즘 | 특정 상황에서 전체적으로 최소 비용을 보장하며, 비용 중심 탐색에 적합함 |
계산 시간이 길고 메모리 사용량이 많으며, 휴리스틱 접근이 불가하여 비효율적일 수 있음
|
| A* | 휴리스틱 탐색 기법을 사용하는 최단경로 찾기 알고리즘 | 적절한 휴리스틱 함수를 사용하면 효율적이고 빠른 경로 찾기 가능함, 탐색 시간복잡도와 메모리 사용이 적음 |
휴리스틱 함수의 선정이 중요하며, 적합하지 않은 함수를 사용하면 성능이 저하됨
|
Greedy 알고리즘
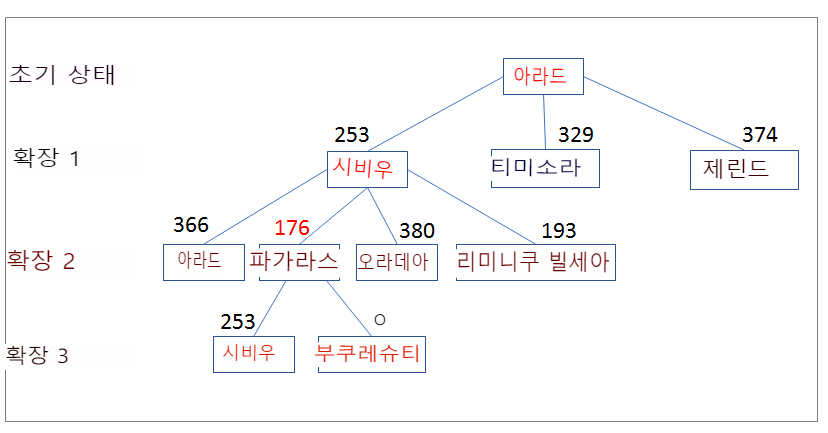
1. Greedy 알고리즘의 기본 개념
Greedy 알고리즘은 매 단계에서 최적 선택을 하는 탐색 알고리즘으로, 현재 상태에서만 가장 높은 점수 혹은 낮은 비용을 가지는 선택지를 선택합니다 이 알고리즘은 간단하고 빠르지만, 전체적인 최적해를 찾지 못하는 경우가 많습니다.
2. Greedy 알고리즘 작동 원리
- 탐색 과정에서 가능한 후보 상태를 생성합니다.
- 각 후보 상태에 점수 or 비용을 계산하고, 최상의 점수(최소 비용)를 가지는 상태를 선택합니다.
- 선택된 상태가 목표 상태에 도달할 때까지 과정을 반복합니다.
3. Greedy 알고리즘 장단점
장점
- 계산 속도가 빠르며 구현이 쉽습니다.
- 합리적인 해를 빠르게 찾을 수 있습니다.
- 빠른 의사결정이 필요한 상황에 적합합니다.
단점
- 전체적인 최적해를 찾지 못하는 경우가 많습니다.
- 지역 최적해에 빠진 상태에서 빠져나지 못합니다.
- 특정 문제에서는 효율성이 떨어집니다.
4. 적절한 적용 사례와 대안 알고리즘 선택
Greedy 알고리즘은 휴리스틱 법칙을 활용하여 문제를 근사적으로 풀어나가는 경우에 사용할 수 있습니다. 그러나, 이러한 알고리즘이 탐색을 조기에 마감하므로 전체적인 최적해를 찾지 못하는 경우가 있습니다. 그렇기 때문에 문제에 따라 DP(Dynamic Programming), 분기 및 정복(Branch and Bound) 및 A* 알고리즘 등의 다양한 최적화 알고리즘 사용하여 최적해를 찾아야할 필요가 있습니다.
Uniform Cost 알고리즘

1. Uniform Cost 알고리즘의 기본 개념
Uniform Cost 알고리즘은 경로의 발생하는 비용을 동일하게 취급하는 탐색 알고리즘입니다. 이 알고리즘은 경로 상에 각각 다른 비용이 있지만 일일이 비용을 계산하지 않고, 경로에서의 누적 비용을 기반으로 탐색을 수행합니다.
2. Uniform Cost 알고리즘 작동 원리
- 탐색 과정에서 가능한 후보 경로를 생성합니다.
- 각 경로의 누적 비용을 계산하고, 최소 누적 비용을 가지는 경로를 선택합니다.
- 선택된 경로가 목표 도달할 때까지 과정을 반복합니다.
3. Uniform Cost 알고리즘 장단점
장점
- 특정 상황에서 전체적으로 최소 비용을 보장합니다.
- 비용 중심 탐색에 적합합니다.
단점
- 계산 시간이 길고 메모리 사용량이 많습니다.
- 휴리스틱 접근이 불가능하여 경우에 따라 비효율적일 수 있습니다.
4. 적절한 적용 사례와 대안 알고리즘 선택
Uniform Cost 알고리즘은 동일한 비용의 탐색이 필요한 경우에 효율적으로 사용할 수 있습니다. 그러나 다양한 비용이 존재하는 경우 이 알고리즘만으로는 최적화가 어려울 수 있으므로, 그런 경우에는 A* 알고리즘과 같이 휴리스틱 접근이 가능한 알고리즘을 함께 사용하여 탐색 성능을 개선할 수 있습니다.
A* Star알고리즘
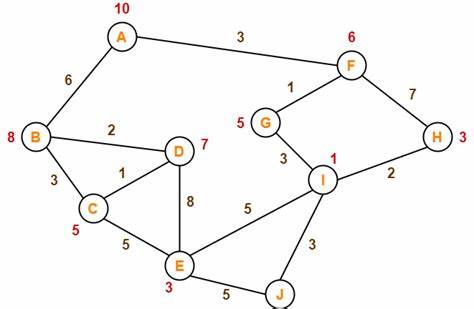
1. A* 알고리즘의 기본 개념
A* 알고리즘은 휴리스틱 탐색 기법을 사용하는 최단경로 찾기 알고리즘입니다. 현재의 상태에서 목표 상태까의 추정 거리를 이용해 탐색 과정에서 어떤경로를 선택할지 결정합니다. 이러한 휴리스틱 정보를 사용함으로써 탐색 과정의 시간복잡도와 메모리 사용량을 줄일 수 있습니다.
2. A* 알고리즘 작동 원리
- 탐색 과정에서 가능한 후보 경로를 생성합니다.
- 이동 비용(g(n))과 휴리스틱 비용(h(n))을 합산한 평가함수 f(n) = g(n) + h(n)을 계산합니다.
- 평가함수 f(n)이장 작은 경로를 선택하고, 목표에 도달할 때까지 이 과정을 반복합니다.
3. A* 알고리즘 장단점
장점
- 적절한 휴리스틱 함수를 사용하면 효율적이고 빠른 경로탐색이 가능합니다.
- 일반적인 탐색에 비해 시간복잡도와 메모리 사용량이 적습니다.
단점
- 휴리스틱 함수의 선정이 중요하며, 적합하지 않은 함수를 사용하면 성능이 저하됩니다.
- 모든 상황에서 최적해를 보장하지는 않습니다.
4. 적절한 적용 사례와 대안 알고리즘 선택
A* 알고리즘은 많은 탐색 및 경로 찾기 문제에 적용할 수 있지만, 휴리스틱 함수가 필수적입니다 따라서 휴리스틱 함수를 선정할 수 없는 상황에는 Dijkstra 알고리즘이나 다른 유형의 알고리즘을 사용하는 것이 더 효율적일 수 있습니다.
탐색 알고리즘 비교 기준
| 탐색 알고리즘 | Optimality | Completeness | 공간 복잡도 | 시간 복잡도 |
| Greedy | 아니오(No) | 아니오(No) | O(b^d) | O(b^d) |
| Uniform Cost | 예(Yes) | 예(Yes) | O(bC/h) | O(b^1+⌈C/h⌉) |
| A* | 예(Yes) | 예(Yes) | O(b^d) | O(b^d) |
- 시간 복잡도(Time complexity): 알고리즘이 얼마나 빠른 시간 안에 문제를 해결하는지를 나타내는 척도입니다. 일반적으로 더 낮은 시간 복잡도를 갖는 알고리즘이 더 빠른 성능을 보여줍니다.
- 공간 복잡도(Space complexity): 알고리즘이 메모리 사용량에 대한 척도입니다. 더 적은 메모리를 사용하는 알고리즘은 일반적으로 더 효율적입니다.
- Optimality: 알고리즘이적의 해를 찾을 수 있는지 여부를 평가하는 기준입니다. 최적의 해를 찾는 알고리즘은 문제에 대한 해결의 질이 더 높습니다.
- Completeness: 알고리즘이 어떤 입력에 대해서도 문제를 해결할 수 있는지를 나타내는 척도입니다. 완전한 알고리즘은 모든 경우에 대해 정한 결과를 도출해냅니다.
- Scalability: 알고리즘이 입력 크기가 증가함에 따라 얼마나 잘 확장 가능한지를 평가하는 기준입니다. 처리할 문제 크기가 커질 때 알고리즘이 얼마나 효율적으로 작동하는지를 나타냅니다.
- Robustness: 알고리즘이 다양한 문제에 적용할 수 있는 지표로, 입력 데이터가 가질 수 있는 다양한 상황에 얼마나 잘 대처하는지를 평가합니다. 이에 따라 알고리즘의 활용 범위가 확장됩니다.
- Ease of implementation: 알고리즘을 구현하기 쉬운지를 평가하는 기준입니다 구현이 쉬운 알고리즘은 개발자에게 시간과 노력을 절약해줍니다.
A* 알고리즘과 Uniform 알고리즘 비교
A* 알고리즘은 Uniform Cost Search (UCS) 알고리즘과 유사하지만, 노드의 확장의 순서를 선택하는 방법에 차이가 있습니다.
Uniform (UCS) 은 경로 비용을 기준으로 더 적은 비용을 가지는 노드를 먼저 확장하는 반면, A* 알고리즘은 경로 비용과 휴리스틱 함수로 추정한 목표 노드까지의 예상 비용을 동시에 고려하여 노드를 확장합니다.
즉, A* 알고리즘은 확장의 우선 순위를 결정하는 데 휴리스틱 함수를 사용하므로 UCS보다 더 많은 노드를 찾을 수 있습니다. 그나 허용 가능한 휴리스틱 함수를 사용하면 A* 알고리즘은 여전히 optimal 및 complete하며, 목표 노드에 도달 경로가 경로 비용을 기준으로 가장 최소값일 가능성이 높습니다.
A* 알고리즘은 UCS보다 더 높은 시간 복잡도를 가지고 있지만, 휴리스틱 함수를 사용하면 노드 확장 순서를 더 효과적으로 선택할 수 있도록하므로, 최적 경로를 찾는 데 더욱 효과적일 수 있습니다.
다음 글에서는 직접 탐색 알고리즘을 적용하여 실제로 비교하는 과정을 알아 보겠습니다.
'컴퓨터과학/인공지능' 카테고리의 글 목록
모든 분야의 정보를 담고 있는 정보의 호텔입니다. 주로 컴전기입니다.
jkcb.tistory.com